असं म्हणतात, की जगामध्ये सर्वाधिक प्यायल्या जाणाऱ्या पेयांमध्ये चहाचा नंबर पाण्याच्या खालोखाल लागतो. चहाचे प्रकार आणि करण्याची पद्धत यामध्ये जगभरात प्रचंड विविधता आहे. आपल्यापैकीही बऱ्याच जणांना आपण करतो तीच पद्धत योग्य असे वाटते, आणि त्याच प्रकारचा चहा सहसा आपण पिण्यास प्राधान्यही देतो. दूध घालून केलेल्या चहामध्येही चहा, पाणी, दूध आणि साखरेचे प्रमाण, यांचे गुणोत्तर प्रत्येकाच्या आवडीप्रमाणे वेगवेगळे असू शकते, नव्हे, असतेच म्हणायला हवं खरं तर. मात्र याच चहामुळे, किंबहुना चहा बनवण्याच्या विशिष्ट पद्धतीमुळे घडलेला एक किस्सा संख्याशास्त्राच्या ‘Design of Experiments’ या शाखेमध्ये अत्यंत मूलभूत असे बदल घडण्याची नांदी ठरला असे म्हणण्यास वावगे ठरणार नाही.
ही सुमारे १९२० च्या दशकातली गोष्ट. झालं असं, की एकदा सर रोनाल्ड फिशर, ज्यांना आधुनिक संख्याशास्त्राचा प्रणेता मानलं जातं, त्यांची डॉ. म्युरीएल ब्रिस्टॉल नावाच्या एका जीवशास्त्रज्ञाबरोबर कुठल्यातरी कामासंदर्भात चर्चा सुरू होती. ही चर्चा साधारण दुपारी चहाच्या वेळेला चालली होती. साहजिकच तेव्हा सर रोनाल्ड फिशर यांनी डॉ. ब्रिस्टॉलना मोठ्या अदबीने चहा देऊ केला. मात्र तेव्हा एक गंमत झाली. फिशर यांनी चहाच्या कपात प्रथम दूध ओतलं आणि नंतर चहा ओतला. ब्रिस्टॉल कसल्या खट! त्यांनी तो चहा प्यायचा चक्क नाकारला. फिशरना थोडा धक्काच बसला, त्यांनी विचारलं, काय झालं म्हणून. तेव्हा ब्रिस्टॉलनी उत्तर दिलं, की त्यांना कायम प्रथम कपामध्ये चहा आणि नंतर त्यात दूध घालून पिण्याची सवय आहे, आणि त्यांना अगदी तसाच चहा लागतो. झालं! फिशरना आला राग.

खरं तर चहा आधी की दूध आधी (कोंबडी आधी की अंड आधी च्या चालीवर वाटतं नाही?) हा वाद त्यावेळी ब्रिटनमध्ये तसा अगदी जुना होता, अगदी तिथे चहाचं आगमन जेव्हा १७व्या शतकात झालं अगदी तेव्हापासून! चहा करावा कसा हा मुद्दा खरं तर आजतागायत तसाच विवादास्पद आहे, अगदी त्यावरूनच तुंबळ युद्ध भडकण्याची शक्यताच म्हणा ना हवं तर. असो.
तर फिशर पडले विज्ञानवादी. त्यांचं असं मत पडलं, की हा मुद्दा अगदीच निरर्थक आहे; अ मध्ये ब मिसळलं काय किंवा ब मध्ये अ काय, शेवटी जो परिणाम उत्पन्न होणार तो (thermodynamically) सारखाच असणार ना! (बहुधा त्यावेळी याचं रसायनशास्त्र-दृष्ट्या फार संशोधन झालं नसावं; सध्या मात्र याबद्दल काहीशी माहिती उपलब्ध आहे). त्यांच्या मते चहामधलं दुधाचं प्रमाण आणि तापमान शेवटी सारखंच राहणार. त्यांनी तोच मुद्दा पकडून ठेवला, ते म्हणाले चहा आणि दुधाच्या क्रमाने काहीही फरक पडणार नाही.

ब्रिस्टॉल मात्र आपल्या मुद्द्यावर ठाम होत्या. त्या म्हणाल्या, ‘चवीत फरक पडतो, वाटलं तर मी सिद्ध करायला तयार आहे. मला वेगळ्या पद्धतीने बनवलेला चहा निश्चितच ओळखू येईल चवीतल्या फरकामुळे.’ फिशरचा तरीही त्यांच्यावर विश्वास बसत नव्हता. त्यांना ही गोष्ट अशक्यच वाटत होती. आता या वादाला काही अंत राहिला नसता, कारण दोघेही हटवादी! कोणीच मुद्दा सोडायला तयार नव्हतं. तेव्हा त्यांच्या या भांडणामध्ये विल्यम रोच नावाचे रसायनशास्त्रज्ञ धावून आले. ते म्हणाले, आपण असं करुयात, आपण ब्रिस्टॉलची परीक्षाच घेऊ. दोन्ही पद्धतीनी चहा बनवून ब्रिस्टॉलना प्यायला लावू आणि बघूयात त्यांना ओळखता येतोय का ते! फिशर आणि ब्रिस्टॉल दोघांनाही ही कल्पना पसंत पडली.
त्याकाळी मुळातच फिशर कृषीविषयक डेटा विश्लेषक म्हणून कार्यरत होते. यासंदर्भात त्यांनी विविघ पिकांचं उत्पन्न, त्या उत्पन्नातील तुलनात्मक फरक (variation) याविषयी सखोल अभ्यास करून विविध शोधनिबंध प्रसिद्ध केले होते. Design of Experiments (किंवा प्रयोग-आखणीचं शास्त्र) याचा फिशरचा नुसता अभ्यासच नव्हता, तर त्यामध्ये त्यांनी नवीन संख्याशास्त्रीय कसोट्यांची (ANOVA) बहुमोल भरही घातली होती.
ब्रिस्टॉलच्या दाव्याची अचूक शहानिशा करण्यासाठी त्यांनी त्याच धर्तीवर प्रयोगाची आखणी केली. Replication, randomisation, blinding ही Design of Experiments मधली काही प्रमुख तत्वे. फिशरनी काय केलं, की दोन्ही प्रकारचा चहा – आधी चहा मग दूध असे चार आणि आधी दूध मग चहा असे चार – असे एकूण आठ कप तयार केले आणि ते अनिश्चित अनुक्रमाने (randomly) ब्रिस्टॉलना चाखू दिले. आश्चर्याची गोष्ट अशी की दोन्ही चहातला फरक ब्रिस्टॉलनी आठही वेळा अचूक ओळखला. झाल्या प्रकारामुळे फिशर फारच बुचकळ्यात पडले. त्यांचे आडाखे चुकले होते. ब्रिस्टॉलचा विजय हा फिशर साठी जरा अपमानास्पद होताच, पण या प्रकाराने त्यांना सखोल विचार करायला भाग पाडलं. प्रथम त्यांना वाटलं, की केवळ सुदैवाने (by luck) तर ब्रिस्टॉल यशस्वी झाल्या नसतील काय? फक्त योगायोगाने आठही वेळा अचूक ओळखण्याची शक्यता काय? त्यांनी असं घडण्याची शक्यता पडताळण्यासाठी चक्क एक गणित मांडलं.
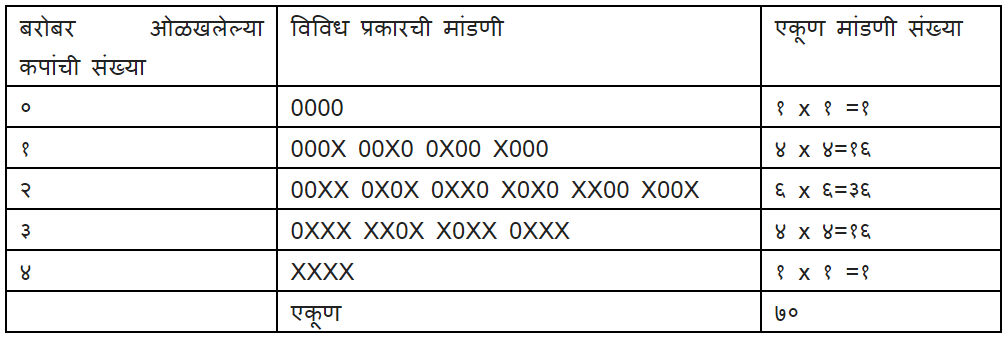
समजा असं गृहीत धरूयात, की चहा पिणाऱ्याला (इथे ब्रिस्टॉलना) चवीतला फरक कळत नाही. आता आठापैकी चार कप हे विशिष्ट पद्धतीचे होते – आधी चहा आणि मग दूध. हे चारही कप अचूक ओळखणे म्हणजेच उर्वरित आधी दूध व नंतर चहा घालून तयार केलेले चार ओळखण्यासारखेच आहे. चारपैकी जितके जास्त कप ओळखता येतील तितका वरील गृहितकाला छेद देणारा पुरावा सबळ होत जाईल. आता प्रथम हे ओळखता येण्याचे शक्य तितके सगळे combinations विचारात घ्यायला हवे. वरील गृहीतक योग्य आहे असे मानल्यास हे किती पद्धतीने शक्य आहे? चारपैकी एकही बरोबर न ओळखणे, एकदाच बरोबर ओळखणे, २,३ किंवा चारही अचूक ओळखणे असे प्रकार लक्षात घेतले तर Combination च्या सूत्रानुसार ही संख्या ८!/(४!*४!) = ७० इतकी येते. (इथे ! हे factorial संदर्भात वाचवे). हे समजून घेण्यासाठी खाली दिलेली मांडणी उपयुक्त ठरेल.
सर्वात महत्त्वाचं म्हणजे वरील गृहीतक बरोबर असल्यास चारही कप केवळ आणि केवळ योगायोगाने (by chance) बरोबर ओळखण्याची शक्यता १/७० (६.२५%) इतकी कमी आहे! म्हणजे ब्रिस्टॉलना दोन्ही प्रकारच्या चहाच्या चवीत फरक करता येत असावा तर.
फिशर या प्रयोगाचा विचार करताना इथेच थांबले नाहीत. त्यांनी यांचा अधिकाधिक खोलात जाऊन विचार केला. इथे हे लक्षात घ्यायला हवं की वर मांडलेले गृहीतक खोडून काढण्यासाठी काहीतरी सुस्पष्ट सांख्यिकी निकष लावणे गरजेचे आहे. त्यांच्या असं लक्षात आलं की कप ओळखताना समजा एखादी चूक झाली तर? मग अशा किती चुका केल्या तरी या प्रयोगातून मूळ गृहितकाचे खंडन करण्यासाठी पुरेसा खात्रीलायक निष्कर्ष काढत येऊ शकेल? ‘ब्रिस्टॉलना चवीतला फरक कळत नाही’ हे गृहीतक खोडण्यासाठी ‘ब्रिस्टॉलनी चारही कप बरोबर ओळखणे गरजेचे आहे’ की ‘ब्रिस्टॉलनी चारपैकी किमान तीन कप बरोबर ओळखणे पुरेसे आहे’ या दोन पैकी कोणती कसोटी किमान गरजेची आहे? वरच्या मांडणीचा विचार केला, तर चवीतला फरक कळत नसताना चार पैकी चारही बरोबर ओळखणे यांची शक्यता १/७० (६.२५%) आहे. समजा चारपैकी एकच कप ओळखायचा चुकला तर ही शक्यता १/७० वरुन १६/७० इतकी येते. म्हणजे किमान तीन कप ओळखण्याची शक्यता (१६+१)/७०, जवळपास २४%. याचा अर्थ, चवीतला फरक कळत नसतानाही किमान तीन कप बरोबर ओळखण्याची शक्यता बरीच जास्त (२४%) आहे. आता, ही शक्यता जितकी कमी तितका फरक न कळण्याच्या गृहितकाविरुद्ध जाणार पुरावा अधिक सबळ. या केसमध्ये, २४% शक्यता ही खूप मोठी असल्याने ‘फरक कळत नाही’ यांचे खंडन करण्यासाठी हा पुरावा कमी खात्रीशीर ठरतो. म्हणजे एक विशिष्ट प्रकारचे ४ कप असल्यास, चारही अचूक ओळखणे सिद्धतेच्या दृष्टीने जास्त आवश्यक आहे.
त्यांनी मग थोडा आणखी विचार केला. समजा आठ कप (चार अधिक चार) ऐवजी बारा कप (सहा अधिक सहा) घेतले असते तर? तर ही कसोटी आधीपेक्षा जास्त कठीण आणि म्हणूनच अधिक काटेकोर झाली असती. चवीतला फरक कळत नसताना सहाही कप अचूक ओळखण्याची शक्यता १/९२४ इतकी कमी आहे. सहापैकी किमान पाच बरोबर ओळखण्याची शक्यता ३७/९२४ (४%). (याची ताळेबंद मांडणीही वरच्या मांडणीच्या अनुषंगाने करता येईल). या परिस्थितीमध्ये एक आडाखा चुकला तरीही ही चूक तितकीशी हानिकारक नाही. याचा अर्थ, जितका sample size जास्त, तितकी ही कसोटी उत्तमोत्तम साबीत होऊ शकते. फिशरच्या लक्षात आले की ही कसोटी विविध क्लिष्ट प्रॉब्लेम्समध्ये समर्पक ठरू शकते. याच कसोटीला आता फिशरची अचूक चाचणी (Fisher’s Exact Test) म्हणून ओळखले जाते.
पुढील काही काळात फिशरने या प्रयोगाच्या आखणीच्या अनुषंगाने अधिकाधिक पैलूंचा बारकाईने अभ्यास केला. १९२० च्या दशकात ही जेव्हा घडली, त्याआधी वैज्ञानिक प्रयोगांची सांख्यिकीमापन दृष्टीने आखणी, डेटा विश्लेषणाच्या पद्धती, यामध्ये कमी सुस्पष्टता होती. फिशरच्या संशोधनाने या सर्व पद्धतींमध्ये मोलाची भर पडली. चहावरून सुरू झालेल्या एक छोट्याशा पैजेचे संख्याशास्त्रात इतके महत्त्वाचे योगदान असेल हे कोणाला सांगून तरी खरे वाटेल काय?
- मेघना
(हा लेख माझ्या ब्लॉगवरही प्रकाशित केला आहे.)

रोचक आहे!
रोचक आहे!
फारच मस्त माहिती! लेख आवडला!
फारच मस्त माहिती! लेख आवडला!
वाह सही आहे
वाह सही आहे
मी अजूनही त्या चहा आधी की दूध यामध्येच अडकलो आहे
छान लिहिला आहे लेख..
छान लिहिला आहे लेख..
Interesting.
Interesting.
Interesting !
Interesting !
फारच भन्नाट !!
फारच भन्नाट !!
अॅनोव्हा आणि डिझाईन ऑफ एक्स्पेरिमेंट मागे इतकी भारी गोष्ट आहे हे माहितीच नव्हते. या गोष्टी सध्या व्हॅक्सिन आणि औषधांच्या ट्रायलबद्दल खुप बातम्यांमध्ये येत आहेत. त्यांच्या बद्दल काही गोष्टी असतील तर त्या सुद्धा लिहा.
छान लिहिलाय लेख.
छान लिहिलाय लेख.
>>जितका sample size जास्त, तितकी ही कसोटी उत्तमोत्तम साबीत होऊ शकते.>> हे इंट्युटिव्हच आहे ना? यात काही थ्रेशोल्ड आहे का? अर्थात ते सर्वसमावेशक असणार नाही आणि प्रॉब्लेम्स प्रमाणे किती एरर रेट टॉलरेट होईल ते बदलेल. पण तरी काही ठोकताळे आहेत का?
छान
छान
मस्त लेख.
मस्त लेख.
मस्त!
मस्त!
टिक टॉक नव्हता तेंव्हा लोक
टिक टॉक नव्हता तेंव्हा लोक असा टाईमपास करायचे तर...
वावे, जिज्ञासा, ऋन्मेऽऽष,
वावे, जिज्ञासा, ऋन्मेऽऽष, रूपाली विशे - पाटील , अनिता, मंजूताई, धनि, अमितव, BLACKCAT, निनाद आचार्य, सीमंतिनी आणि च्रप्स- लेख आवर्जून वाचून अभिप्राय दिल्याबद्दल आभारी आहे.
@धनि , माझ्या औषधशास्त्रातील गाढा अभ्यास नाही, पण संख्याशास्त्राच्या दृष्टिकोनातून लिहायचा नक्की विचार करेन.
@च्रप्स, हाहाहा
@अमितव
@अमितव
हे इंट्युटिव्हच आहे ना? >> नक्कीच. जेव्हा sample size कमी असतो तेव्हा थोड्याशा फरकाने देखील अनुमानाच्या गुणवत्तेत बराच फरक पडू शकतो हे वरच्या उदहरणातून अधोरेखित करायचं होतं मला. उदा. चार ऐवजी सहा याने जितका फरक पडेल तितका फरक शंभर चे एकशे दोन होताना पडणार नाही. कुठल्याही चाचण्या कमी sample size साठी sensitive असतात.
यात काही थ्रेशोल्ड आहे का? >> एक थ्रेशोल्ड असा नक्कीच नाही, तुम्हीच म्हणल्याप्रमाणे प्रॉब्लेम नुसार गरज बदलू शकते.
बहुतेक वेळी २५-३०च्या आसपास किंवा जास्त असलेला बरा असं म्हणतात.
पण तरी काही ठोकताळे आहेत का? >> हो. आहेत. तुमच्याच प्रतिसादात म्हटल्याप्रमाणे 'एरर' हा महत्त्वाचा भाग असतो. significance level, statistical power, variance , margin of error यांचा sample size शी सहसंबंध असतो. त्यामुळे सहसा, (उदाहरणार्थ) significance level ५% किंवा statistical पॉवर कमीत कमी ९५% अथवा margin of error १% इत्यादी प्रथम ठरवलं जातं आणि मग ही साध्य करण्यासाठी किमान किती sample लागेल हा आकडा ठरवता येतो.
या सर्व गोष्टींच्या मागे काही सिद्धांत/नियम आहेत. ते विस्ताराने सांगणं म्हणजे फाफटपसारा वाढायची भीती आहे, त्यामुळे इथेच थांबते.
खूप छान रोचक माहिती मिळाली
खूप छान रोचक माहिती मिळाली मेघना. !
!
ब्रिस्टाल बाईंसारखे taste buds प्रत्येकाला असतीलच असे नाही असे वाटले. But some credit goes to her taste buds and हट्टीपणा
खूप आभार तुमचे.
मी नेहमी आधि दुध घालते कपात.
मी नेहमी आधि दुध घालते कपात.
अशाप्रकारे दुध जास्त चांगले मिसळले जाइल असे मल वाटते.
दुध वरुन टाक्ले तर खाली चहा काळा राहतो कधी कधी.
अर्थात काहिना तो आवडत असावा.
मला तर बाई चहा आणि दूध एकत्र
मला तर बाई चहा आणि दूध एकत्र उकळूनच छान वाटतो चहा... हे वरून दूध.. खालून दूध... मजा येत नाही...
दुध वरुन टाक्ले तर खाली चहा
दुध वरुन टाक्ले तर खाली चहा काळा राहतो कधी कधी.
अर्थात काहिना तो आवडत असावा.
>>>
असं होत नसावे बहुधा. दूधाचा एक थेंब टाकला तरी तो कपभर फिरून येतो.
बाकी मला दूधातच साखर चहापावडर टाकून उकळवलेला चहा आवडतो. यात पाणी वाचवा अभियानालाही हातभार लागतो.
छान माहिती
छान माहिती
लेख उत्तम आहे. धन्यवाद.
लेख उत्तम आहे. धन्यवाद.
तुमच्या ब्लॉग चा दुवा देता का?
मस्तच लेख आणि शिर्षकही चपखल
मस्तच लेख आणि शिर्षकही चपखल अगदी
मला तर बाई चहा आणि दूध एकत्र
मला तर बाई चहा आणि दूध एकत्र उकळूनच छान वाटतो चहा >>
मला रोज दोन कप चहा लागतो!
- धनंजय माने
मी_अस्मिता, निलिमा, चिन्नु,
मी_अस्मिता, निलिमा, चिन्नु, chanchal, हर्पेन आणि हरचंद पालव, अभिप्रायासाठी मनापासून आभारी आहे.
@ मी_अस्मिता - मलाही खरंच कमाल वाटली त्यांच्या हट्टीपणाची.
@chanchal . नक्की. विपु करते.
@ निलिमा, च्रप्स, ऋन्मेऽऽष आणि हरचंद पालव - मी पण चहाप्रेमी आहे! मला छान नीट उकळलेला आवडतो शक्यतो नंतर दूध घालून. इंग्रजांकडे जसं कच्च दूध वापरतात तसं अजिबात आवडत नाही, चहामध्ये दुधाची कच्ची चव अजिबातच नावडती आहे.
@ऋन्मेऽऽष - गवळ्याने आधीच दुधात पाणी मिसळले असले तर
could you pls share your blog
could you pls share your blog link ...
https://www.youtube.com/watch
https://www.youtube.com/watch?v=Fhuc6qOGNPc
हा विडियो नुकताच बघितला आणि हसून हसून मुरकुंडी वळली. विशेषतः ४.५९ च्या पुढे. जगात भारी शोध लावल्याचा आविर्भाव! कमेंट्स ही मजेशीर आहेत.
हे आज वाचले- रंजक, रोचक !
हे आज वाचले- रंजक, रोचक !
माणसाने हट्टी असावे आणि चवींबद्दल सजग.
अनिंद्य, प्रतिसादाबद्दल
अनिंद्य, प्रतिसादाबद्दल मनापासून आभार.
माणसाने हट्टी असावे आणि चवींबद्दल सजग >> अगदी अगदी. तुमच्यासारख्या रसिक आणि खवय्या व्यक्तीकडून ही दाद येणे अगदी स्वाभाविकच
खूप छान लेख. आजच वाचला .
खूप छान लेख. आजच वाचला .
खूपच माहितीपूर्ण .
खूपच माहितीपूर्ण .
आज पुन्हा वाचला लेख,
आज पुन्हा वाचला लेख, ब्रिस्टॉल (मी ब्रिस्टल लिहिले असते) आणि फिशर प्रयोगांची रोचकता अजिबात कमी नाही झालेली
Pages