
भारतीय गणिती श्रीनिवास रामानुजन ह्याच्या आयुष्यात घडलेला एक प्रसंग पुढे देतो. ह्या प्रसंगाच्या अनुषंगाने आलेल्या कोड्याची मजा आपण ह्या लेखात घेऊ.
इंडियन स्टॅटिस्टिकल इन्स्टिट्यूटचे संस्थापक पी. सी. महालनोबिस आणि रामानुजन समकालीन होते. केंब्रिजमध्ये हे दोघे काही काळ एकत्र होते. एकदा रामानुजनच्या घरी असताना महालनोबिस एक कोडे सोडवत होता. त्याने बराच वेळ विचार करून ते सोडवले, तेव्हा रामानुजन स्वयंपाकघरात चुलीवर रसम ढवळत होता. महालनोबिस त्याला म्हणाला, "आज मी एक मस्त कोडं सोडवलंय. तुला विचार करायचा का त्यावर?" रामानुजन काम करता करताच म्हणाला, "बोल की!" ह्यावर महालनोबिसने सांगितलेले कोडे पुढीलप्रमाणे -
एका रस्त्यावर ५० ते ५०० च्या दरम्यान संख्येने काही घरे आहेत. घरांचे क्रमांक १ पासून सुरू होऊन १, २, ३, ... असे क्रमाने वाढत जातात. ह्या रस्त्यावर घर क्र. १ पासून सुरवात करून चालता चालता एका घरापाशी आल्यावर असे लक्षात येते, की त्या घराच्या डावीकडे असलेल्या घरांच्या क्रमांकांची बेरीज आणि त्या घराच्या उजवीकडे असलेल्या घरांच्या क्रमांकांची बेरीज समान आहेत! (दोन्ही बेरजांत त्या घराचा क्रमांक धरलेला नाही.) तर त्या घराचा क्रमांक आणि घरांची एकूण संख्या सांगा.
महालनोबिसला स्वतःला हे करायला बराच वेळ लागला होता. पण आश्चर्याची गोष्ट म्हणजे अगदी हे कोडे सांगताक्षणीच रामानुजन उद्गारला, "घे उत्तर लिहून!" आणि त्याने महालनोबिसला असे एक सूत्र सांगितले, की त्याने ५० ते ५००च काय, पण त्या कक्षेबाहेरीलही सर्व अगणित उत्तरे मिळतील!
काय आहे ह्या कोड्याचे उत्तर? आणि काय असेल ते सूत्र?
------------------------------------------------------
उत्तराबद्दल विचार कसा करावा, ह्याबद्दल थोडा साधा विचार -
जर घरांची एकूण संख्या m मानली, व त्या घराचा क्रमांक n मानला, तर आपल्याला पुढील समीकरण हवे आहे -
![]()
१ पासून क्रमाने संख्यांच्या बेरजेचे सूत्र आपण कधीकाळी शाळेत पाहिलेले आहे. ते वापरून हेच समीकरण पुढील प्रकारे लिहिता येते -
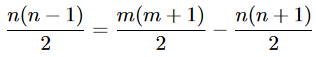
ह्याला २ ने दोन्ही बाजूंना गुणून व थोडीफार बेरीज-वजाबाकी करून ह्या समीकरणास पुढील रूप देता येते -
![]()
ह्यात थोडं नवीन नामकरण करून ह्याला आपण जरा सोपं करू.
![]()
![]()
आणि मग आपल्याला मिळेल ते सुप्रसिद्ध 'ब्रह्मगुप्त-पेल समीकरण' -
![]() .... (*)
.... (*)
अर्थात, ह्या समीकरणाच्या आपल्याला पूर्णांकांत उकली शोधायच्या आहेत, म्हणजे x आणि y हे दोन्ही पूर्णांकच असले पाहिजेत.
आता काय विचार करावा बरे? समजा वरील समीकरणाऐवजी आपल्याला त्यात १ ऐवजी ०, म्हणजे अगदी थोडासाच बदल करून मिळालेले पुढील समीकरण सोडवता येईल का?
![]()
तर हे समीकरण पूर्णांकांत सोडवता येणार नाही. कारण हेच समीकरण आपण पुढीलप्रमाणे पुनर्लिखित करू शकतो -
![]()
अर्थात,
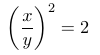
म्हणजेच,
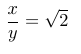
पण आपल्याला माहिती आहे, की २ चे वर्गमूळ अश्या प्रकारे पूर्णांकांच्या भागाकाराच्या रूपात लिहिता येत नाही, कारण ते अपरिमेय आहे.
पण काही हरकत नाही! हे नवीन समीकरण सोडवता येत नाही तर नको येऊ दे! आपलं मूळ समीकरण (*) सोडवता येणार नाही, असं कोणीच म्हटलेलं नाही. पण ह्या समीकरणात आणि मूळ समीकरणात थोडासाच फरक आहे, ह्याचाच अर्थ आपल्या मूळ (*) समीकरणाचं उत्तर x आणि y असेल, तर
![]() हा भागाकार २ च्या वर्गमूळाच्या जवळचा असला पाहिजे! अर्थात, आपल्याला असे दोन पूर्णांक हवेत, ज्यांचा भागाकार २ चे वर्गमूळ तर नाही, पण त्याच्या जवळ जाणारी संख्या असेल. म्हणजे मग आपल्याला x आणि y, व त्यायोगे m आणि n मिळतील.
हा भागाकार २ च्या वर्गमूळाच्या जवळचा असला पाहिजे! अर्थात, आपल्याला असे दोन पूर्णांक हवेत, ज्यांचा भागाकार २ चे वर्गमूळ तर नाही, पण त्याच्या जवळ जाणारी संख्या असेल. म्हणजे मग आपल्याला x आणि y, व त्यायोगे m आणि n मिळतील.
मग? दिसतायत का अशा काही संख्या? ५० ते ५०० जाऊ द्या, पण १ ते १० मध्ये? १० ते १०० मध्ये? खेळा थोडं संख्यांशी आणि बघा मिळतंय का उत्तर!
वरील सर्व बीजगणित आणी विचार रामानुजनने मनात क्षणार्धात केला, व नुसत्या आकडेमोडीनेच नाही, तर सुसूत्र पद्धतीने ह्या प्रश्नाचे उत्तर कसे काढता येईल, ते सांगितले. ते कसे, हे पाहू ह्याच कोड्याच्या उत्तराच्या भागात. तोवर धावू द्या विचारांची गाडी!
वाचकांस नम्र विनंती - तुम्हाला उत्तर मिळाले, किंवा इंटरनेटवर सापडले, तरी प्रतिसादांमध्ये ते लगेच फोडू नका. किंवा सांगायचेच असेल, तर देण्याआधी स्पॉयलर अॅलर्ट द्या. ह्या कोड्याचे उत्तर स्वतः शोधण्यातच त्यामागची गंमत दडली आहे. ती तुम्हीही घ्या, व इतरांनाही द्या. 
(क्रमशः)
(रामानुजनचे छायाचित्र पब्लिक डोमेनमधून साभार)

भाचा की जय हो
भाचा की जय हो
आता एक गंमत. ISI बद्दल.
<<
Because Nehru hired him & because they quickly Googled his name, bhakts are blaming Prasanta Chandra Mahalanobis as the founder of Pakistani intelligence agency, ISI. Morons, it's Indian Statistical Institute that he helped in founding in 1931, which is a govt institute now.
<<
He is viral you know
Ganitatil majechi dhasti
Ganitatil majechi dhasti asalyane pass.
इन्टरेस्टिंग. पुभाप्र.
इन्टरेस्टिंग. पुभाप्र.
भाचा मस्त लेख.
भाचा मस्त लेख. आता 50 ते 500ला प्रोग्रॅम करायला हात शिवशिवतायत, पण उद्या पर्यंत थांबणारे.
आता 50 ते 500ला प्रोग्रॅम करायला हात शिवशिवतायत, पण उद्या पर्यंत थांबणारे.
थोडा स्पॉयलर आहे पुढे.
1 ते 10 मधलं उत्तर विचार करून मिळालं. 10 ते 100 मधलं उत्तर ब्रूट फोर्सने (एक्सेल मध्ये) काढलं. तेव्हा मूळ प्रश्नात 50 ते 500 का म्हटलंय ते समजलं
ते उत्तर आलं की काही सिरीज वगैरे असणार असं वाटतंय.
तू इतकं सोप्या शब्दात लिहिलंयस. मजा आली वाचताना ही.
मस्त लेख
मस्त लेख
स्पॉयलर हिंट
ही हिंट खरंतर लेखातच आहे. एका अपूर्णांकाची किंमत एका अपरिमेय संख्येच्या जवळ जाणारी आहे. अशावेळी कंटिन्यूड फ्रॅक्शन्स (सतत अपूर्णांक?!) वापरणे सोयीचे ठरते.
Ganitatil majechi dhasti
Ganitatil majechi dhasti asalyane pass.

>>>>>+1
गणिती खेळ , खेळ आकड्यांचा, गणितातील गंमतीजमती अशी नावे असणाऱ्या पुस्तकातून शेवटी गणिताचा अभ्यासच बोकांडी बसतो, याचा अनुभव दांडगा आहे
भारी आहे कोडं.
भारी आहे कोडं.
अमितव +1
अमितव +1
मी या कोड्याला पुर्वी घाबरून पास दिला असता. पण भा मुळे मी आज एक्सेलपर्यंत येऊ शकले.
अजून असे लेख यावे ही नम्र ईनंती!
अवांतर : ओ भास्कराचार्य मी
अवांतर : ओ भास्कराचार्य मी मायबोलीवर टाकलेले पैजेचे कोडे अजून कोणी सोडवलेले नाही. तुम्ही सोडवा पाहू. छान आहे ते.
मला पूर्वी कोडी सोडवायला फार आवडायची. आता आयती उत्तर बघायला आवडतात. डोक्याला नसता त्रास होतो. हे तुमच सोडवायचा प्रयत्न करीन.
मस्त कोड आहे रे भाऊ! मी
मस्त कोड आहे रे भाऊ! मी प्रयत्न करायचा प्रयत्न करेन!
Submitted by विक्रमसिंह on 2
Submitted by विक्रमसिंह on 2 July, 2018 - 13:05 >>>>
कुठे आहे ते पैजेचे कोडे? तुमच्या लेखनात तसा धागा दिसला नाही.
कुठे आहे ते पैजेचे कोडे?
कुठे आहे ते पैजेचे कोडे? तुमच्या लेखनात तसा धागा दिसला नाही. >> https://www.maayboli.com/node/21913
सॉरी भास्कराचार्य, विषयांतर झाल्याबद्दल
एक्सेल मधे लगेच येतं उत्तर.
एक्सेल मधे लगेच येतं उत्तर. फॉर्म्युला वगैरे काही नाही झेपला. 1 ते 10 चे उत्तर फॉर्म्युला मधे घालून पाहिल्यावर उत्तर बरोबर येतय ते कळले पण असे उत्तर काढणे कठीण वाटतय.
ते गणित काही डोक्यात शिरणार
ते गणित काही डोक्यात शिरणार नाही.
दोन ओळींमधे आकडे खालील पद्धतीने कोंबले तर ?
पहिली ओळ - १ + ९, ७ + ३ समजा ५ क्रमांकाचे घर या ओळीत आले तर वीस क्रमांकाचे घर या ओळीत
दुसरी ओळ - २ + ८, ६ + ४ दहा क्रमांकाचे घर या ओळीत आणि १५ क्रमांक या ओळीत .. या पद्धतीने प्रत्येक टेबलमधे बेरीज समाज येईल अशा पद्धतीने आकड्यांची विभागणी करीत गेल्यास उत्तर मिळेल असे वाटते.
*****************************
********************************स्पॉयलर आहे ****************************
भा: आत्ता लगेच नको असेल उत्तर तर काढतो.
आता प्रोग्रॅम करुन काढलं तर
8 6
49 35
288 204
1681 1189
9800 6930
या जोड्या मिळाल्या.
आधी काहीच कॉमन झेपत न्हवतं. पण आता एक विचित्र पॅटर्न दिसतोय. :फीलिंग व्हेरी हॅपी:
पुढच्या इटरेशनच्या टोटल दारातुन आधीच्या इटरेशनची टोटल दारं आणि मधलं दार असे दोन्ही आकडे वजा केले तर पुढच्या इटरेशनचे मधले दार येतय.
उ.दा.
1681 - 288 -204 = 1189
9800 - 1681 - 1189 = 6930
हे रेलेवंट आहे का माहित नाही, कारण याने पुढचा नंबर काढायला काहीच मदत होताना दिसत नाहीये. पण एक पॅटर्न दिसला इतकंच. आणि तो दिसल्याने जामच मजा आली.
ओह्ह... आय थिंक आय कॅक्ड ईट.
********************************स्पॉयलर आहे ****************************
ओह्ह... आय थिंक आय कॅक्ड ईट.ऑर मे बी नॉटपण आणखी एक पॅटर्न दिसतोय.
आधीच्या पायरीतील अंकांची बेरीज (उदा. ८ + ६, ४९+३५ इ.) आणि पुढच्या पायरीतील मधल्या दाराचा क्रमांक (उदा. ३५, २०४ इ) यातील फरक हा अंकांच्या बेरजेची दुप्पट आणि पुढच्या पायरीतील एकूण दारे यातील फरका येवढा दिसतोय.
उ.दा.
8 + 6 = 14 आणि 35 मधला फरक = 21
14 * 2 = 28 आणि 49 मधला फरक = 21
तसचं
288 + 204 = 492 आणि 1189 फरक = 697
492 * 2 = 984 आणि 1681 फरक = 697
यातुन पुढचा क्रमांक मिळेल का?
आता हे असे फरक मांडले तर 21, 120, 697, 4060 येत आहेत. या संख्यांत काही साम्य सापडलं तर सुटेल प्रश्न.
एक ते दहा खेळा (डावी बाजु
एक ते दहा खेळा (डावी बाजु घरांची संख्या क्रमांक एक दोन तीन नऊ दहा) (उजवी बाजु घरांची संख्या क्रमांक आठ सात सहा चार पाच) डावी बाजु एकुन बेरिज पंचवीस ,उजवी बाजु एकुन बेरिज तीस , तीस वजा पाच बरोबर पंचवीस म्हणजे त्या घराच क्रमांक पाच
घरांची एकुन संख्या दहा हे तर
घरांची एकुन संख्या दहा हे तर राहिलंच सांगायच
दुसर उत्तर( एक ते सात एकाच
दुसर उत्तर( एक ते सात एकाच लाईनीत म्हणजे ही( डावी बाजु)आता राहिलेले तीन क्रमांक आट नऊ दहा (उजवी बाजु)डावी बाजु एकुन बेरिज अठ्ठावीस ,उजवी बाजु एकुन बेरीज सत्तवीस म्हणजे २८ वजा एक बरोबर २७ म्हणजे घर क्रमांक एक व घरांची संख्या एकुन दहा
भारीच अमितव! तुझ्या सीरिज
भारीच अमितव! तुझ्या सीरिज मध्ये ट्रिव्हिअल सोल्युशन पण धर ना. (१,१) एकच घर आणि त्यामुळे मधले दार सुद्धा क्रमांक १. दोन्ही बाजूंची बेरीज शून्य होते, जी ट्रिव्हिअली समान आहे.
हो हो. 1, 1 पण आहेच. मी
हो हो. 1, 1 पण आहेच. मी प्रोग्रॅमला ते स्किप करायला सांगितलेलें.
पण ते पण उत्तर बरोबर आहेच. ते घालुन आणखी काही क्लु मिळू शकेल कदाचित.
आता परत नजर टाकली तर आणखी एक
आता परत नजर टाकली तर आणखी एक दिसलं की वरील संख्येनंतर (कमित-कमी) २३,००० पर्यंत (कदाचित आणखी बरीच जास्ती पर्यंत ) अशी एकही संख्या नाही.
२३००० नंतर माझा 2Y वर्ग रॅप अराउंड होतोय. प्रोग्रॅम फाईन ट्युन करता येईल. पण त्यातुन काही निष्पन्न होणार असेल तर करीन.. काही होईल असं वाटत नाही.
भा, डझ एनिथिंग मेक्स सेन्स? का भलत्याच दिशेने विचार करतोय? काही दिशा दाखवलिस तर आणखी विचार करता येईल. ऑनलाईन शोधणार नाहीये.
विक्रमसिंह तुम्ही दिलेल्या
विक्रमसिंह तुम्ही दिलेल्या लिंकवर हे पान पहायची परवानगी नाही असा संदेश येत आहे.
स्पॉयलर.
स्पॉयलर.
.
..
.
.
.
.
.
१ ते १० तलं उत्तर कागद न वापरता असंच काढता आलं. ८ घरांतलं सहावं घर. १ ते ५ ची बेरीज १५.आणि ७+८ =१५.
नेमकं कोडं काय आहे ?
नेमकं कोडं काय आहे ?
१ ते ५०० घरं आहेत. दोन्ही बाजूला आहेत. त्यातल्या एका घराजवळ दोन्ही बाजूंची बेरीज समान येते. ते घर एकच आहे ना ?
कि अशा अनेक शक्यतांबद्दल आहे कोडं ? म्हणजे १ ते ५० , १ ते दहा अशा ?
रस्त्याच्या एकाच बाजूला ओळीने
रस्त्याच्या एकाच बाजूला ओळीने घरे आहेत.
ओह. आता स्पष्ट झालं कोडं.
ओह. आता स्पष्ट झालं कोडं.
७ चा आणि याचा काहितरी संबंध
३७३ / ५२७ आणि ६१२ / ८६५ इतक्या जवळ येतात पण एकाने मार खातात.
7ने भाग जाण्याची कायतरी भानगड दिसते. एकतर साताने पूर्ण भाग जातोय किंवा बाकी 1 किंवा 6 उरतेय. रामानुजनचे उत्तर म्हणजे मूळ संख्याचा राडा असणारा 7, 11 13 17 वगैरे
भास्कराचार्य मला एक सोप
भास्कराचार्य मला एक सोप समिकरण सापडल आहे. (पुस्तक किंवा इतर कुठलेही माहिती स्त्रोत न वापरता ) ते वापरून ३०० अंकापर्यंत अशा ३ जोड्या सापडल्या.

त्यातली एक भरत यांनी लिहिलेली ८ - ६. बाकीच्या दोन लिहित नाही. एक १०० च्या खाली आणि दुसरी २०० च्या वर पण ३०० च्या खाली.
३०० नंतर १५०० पर्यंत अजून जोडी नाही. नंतरची एकदम १६८१ - ११८९
नंतर २५०० पर्यंत नाही.
पाहिजे तर अजून टेस्ट करतो.
माझ्या समिकरणात अमितव यांच्या
माझ्या समिकरणात अमितव यांच्या जोड्या बसत आहेत
Pages