अशा विषयावर लिहिताना आड्यन्ससाठी सुरवात हलकीफुलकी करावी असा संकेत आहे. पुण्यात (मायबोलीवर?) सुद्धा जर लोकांना थोडे हसवले नाही तर तो फाऊल धरतात असे ऐकले आहे. ह्या नियमाला जागून -
An Experimental Physicist and a Mathematician meet each other. The Physicist asked the Mathematician - "What area do you study?" He answered - "Knot Theory." Physicist replied - "Me neither!"
प्राथमिक पातळीवर Knot Theory म्हणजे अत्यंत concrete अशा, साध्याशा वाटणार्या, knots अर्थात गाठींचा अभ्यास होय. Knots आपण पाहू शकत असल्याने ह्यातील अनेक गोष्टी समजण्याची प्रेरणा सहज मिळू शकते, तसेच उत्साही लोक अनेक प्रकारे त्यांबरोबर खेळून त्यांचे गुणधर्म स्वतः तपासून पाहू शकतात. ह्या लेखातून अशा साध्या खेळांतून बरीच माहिती कशी मिळवता येते हे पाहण्याचा प्रयत्न करूया.
टीप : Topologists ना अवकाशाच्या आकाराच्या गुणधर्मांचा अभ्यास करावयाचा असतो. सर्वसाधारणपणे अशा अभ्यासात लांबी, क्षेत्रफळ, आकारमान अशा गोष्टींची पर्वा केली जात नाही. तुम्ही अभ्यासत असलेल्या गोष्टीला हळूहळू ताणून वा दाब देऊन कितीही वाकवू शकता, परंतु फाडू किंवा तोडू शकत नाही. तुम्ही बघत असलेल्या गोष्टींमध्ये भोके आहेत का, टोके आहेत काय अशा गुणधर्मांचा अभ्यास केला जातो. ह्याच अनुषंगाने आपण Knots कडे बघणार आहोत.
Knots म्हणजे काय?
सर्वप्रथम Knots किंवा गाठी हे म्हणताना काय अभिप्रेत आहे, हे सांगितले पाहिजे. सगळ्यांनाच दोरीची गाठ म्हणजे काय ते माहीत आहे. परंतु ह्या लेखामध्ये (आणि सर्वसाधारणपणे) मोकळ्या दोर्या असलेल्या गाठी अभिप्रेत नाहीत. वर म्हटल्याप्रमाणे, जर दोर्या मोकळ्या असतील, तर ताणून, गुंता सोडवून कुठलीही गाठ सोडवता येऊ शकते. (खर्या जगातल्या दोर्या पूर्णतः लवचिक नसतात, पण इथल्या असतात.) परंतु एखादी गाठ बंद असेल तर दोरी तोडल्याशिवाय ती सोडवता येणार नाही आणि हे करायची परवानगी नाही. अशा रीतीने सर्व गाठी ह्या closed loops आहेत. उदाहरणार्थ -
(१) Unknot

साधे वर्तुळ ही सुद्धा एक 'गाठ नसलेली' अशी गाठच आहे. म्हणून तिला unknot म्हणतात. तिला trivial knot असेही म्हणता येईल. ह्याविषयी जास्त पुढे येईलच.
(२) Trefoil

Trefoil ही trivial नसलेली सर्वात साधी/पहिली गाठ म्हणता येईल. हीचे नाव क्लोव्हर झाडाच्या पानावरून पडले. ह्या गाठीचे गुणधर्म बरेच रुचीपूर्ण आहेत. उदाहरणार्थ, ह्या गाठीचे आरशातील प्रतिबिंब ही सुद्धा trefoil च म्हणता येईल. परंतु ह्या दोन्ही गाठी एकमेकांशी समान नाहीत! (समान कुठल्या अर्थाने ते येईलच. परंतु त्या दोघींकडे पाहून हे दिसायला हरकत नाही.)
(३) काही Knots
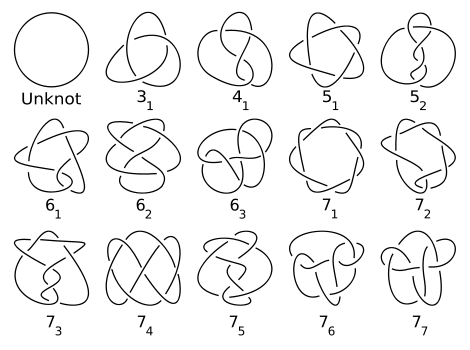
ही अजून काही उदाहरणे. ह्यांची नावे कशी दिली आहेत ते पुढे येईलच. (पण खरे तर तुम्ही स्वतःही अंदाज बांधू शकता!)
कुठले प्रश्न विचारले जाऊ शकतात?
आपण गाठींची उदाहरणे पाहिली. म्हटल्याप्रमाणे ह्या खूप दृश्य असल्याने ह्यांच्याशी निगडित प्रश्न नुसते बघून सोडवता येतील असे वाटू शकते. उदाहरणार्थ, मी वर म्हटले, की, Unknot ही trivial आहे, आणि Trefoil मात्र नाही. हे मी कुठल्या आधारे म्हटले? तर Trefoil शी कितीही खेळ केले, कितीही सोडवायचा प्रयत्न केला तरी तिला साध्या Unknot मध्ये रूपांतरित करता येणार नाही असे वाटते. परंतु ह्या गोष्टीची सिद्धता शोधायचा प्रयत्न केला तर? तुम्ही म्हणाल, जी गोष्ट समोर दिसते आहे, तिची सिद्धता कशाला? परंतु असे गणितात चालत नाही. ते का चालत नाही, ह्यासाठी एक उदाहरण देतो.
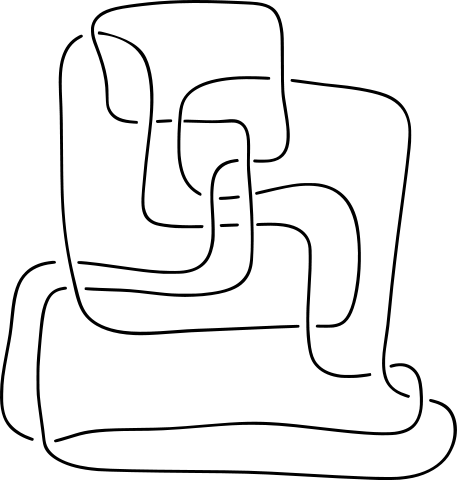
ह्या गाठीचे Unknot मध्ये रुपांतर केले जाऊ शकते असे मी म्हटले तर पहिल्या फटक्यात किती लोक ह्यावर विश्वास ठेवतील? एकंदरीतच ह्यावर किती लोकांचा विश्वास बसेल? परंतु हे खरे आहे.
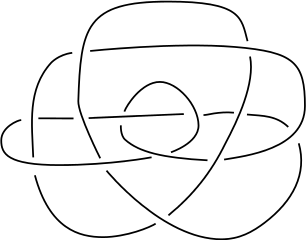
ही अजून एक गाठ, जी Unknot मध्ये रुपांतरित होऊ शकते. हे सुद्धा दिसायला अगदी सहज नाही. किंबहुना, ह्या दोन्ही गाठी एकाच गाठीची वेगळी रुपे आहेत, ह्याचाच अर्थ त्या एकमेकांचीही रुपे आहेत. परंतु हे ह्या दोन्ही गाठींकडे नुसता दृष्टीक्षेप टाकून बहुधा कळणार नाही.
अशा रीतीने "दोन गाठी दिल्या असता त्या वरील अर्थाने समान आहेत की नाहीत हे कसे ओळखायचे?" हा प्रश्न महत्वाचा ठरतो.
हा प्रश्न सोडवण्यासाठी आपण 'गाठींशी खेळतो' म्हणजे नक्की काय करतो ते प्रथम बघू. त्याचा अभ्यास केल्यावर आपल्याला आपला प्रश्न कसा सोडवावा ह्यासाठी काही दिशा मिळू शकेल.
Reidemeister moves
१९२६ मध्ये Reidemeister आणि स्वतंत्रपणे १९२७ मध्ये Alexander आणि Briggs ह्यांनी दाखवून दिले, की गाठी रुपांतरणाचे सर्व प्रयत्न हे फक्त तीन प्रकारच्या साध्या चालींचे sequences अर्थात श्रेणी म्हणून सांगता येऊ शकतात. त्या पुढीलप्रमाणे : (इंग्लिशच्या वापरासाठी येथेही दिलगीर आहे, परंतु चित्र सोबत देत असल्याने त्याचा परिणाम इतका न जाणवावा. नंतर मराठीत चपखल वाक्ये सुचल्यास बदल करीन.)
(१) Twist and untwist in either direction.
(२) Move one loop completely over another.
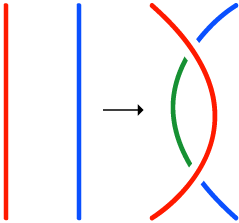
(३) Move a string completely over or under a crossing.
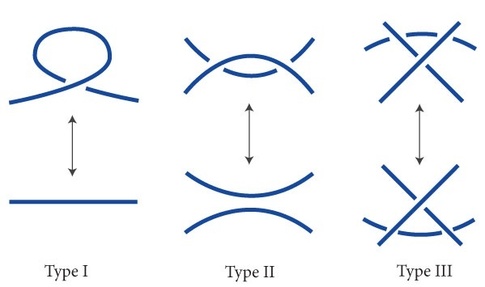
(उदाहरणार्थ एखादी गाठ सोडवण्याचा प्रयत्न क्रमाने १२२३१३१२१३३ असा असू शकतो.)
वरील गोष्ट पचायला थोडी कठीण जाईल कदाचित, परंतु तुम्ही स्वतः खेळ करून पाहिलात, तर ह्याहून काही वेगळे करणे कठीण आहे हे लक्षात येईल आणि खरेच ह्या चालीच पुरतात.
वरील निरीक्षण खूप सुंदर तर आहेच, (प्रत्येक प्रयत्न आपल्याला फक्त तीन प्राथमिक चालींमध्येच सांगता येऊ शकतो) परंतु आधीचा प्रश्न सोडवण्यासाठी देखील ते फार महत्वाचे आहे. कसे ते पुढे बघूया.
Knot Invariants
एका बावळटशा वाटणार्या उदाहरणाने सुरवात करूया. (त्यातून पुरेशी प्रेरणा मिळेल अशी आशा.)
बुद्धिबळातील उंटाची चाल बर्याच जणांना माहित असेल. ते नेहमी तिरपे चालतात. तिरप्या दिशेने ते कोठेही कितीही घरे चालू शकतात. जर एक उंट एका कोपर्यातल्या घरात (समजा पहिल्या आडव्या ओळीतल्या पहिल्या घरात) ठेवला, तर अशा काही चाली खेळता येतील का, जेणेकरून शेवटी तो पहिल्या आडव्या ओळीतल्या आठव्या अर्थात शेवटच्या घरात जाऊन पोहोचेल?
सर्वांच्या लक्षात येईल, की हे शक्य नाही. आणि ह्याचे कारणही सोपे आहे. आठव्या घराचा रंग हा पहिल्या घराच्या विरुद्धच असतो. परंतु उंटाच्या प्रत्येक चालीनंतर तो आधीच्याच रंगाच्या घरात जाऊन पोहोचतो. त्यामुळे आधी एका रंगाच्या घरात सुरवात झाली असता कितीही चाली केल्या, तरी शेवटच्या घराचा रंग बदलणे शक्य नाही आणि म्हणून तो शेवटच्या घरात जाऊ शकत नाही.
अगदी साध्याशा वाट्णार्या ह्या उदाहरणात एका महत्वाच्या गणितीय आराखड्याची बीजे दडली आहेत. आपल्याला एक सुरवातीची जागा आणि काही परवानगी असलेल्या चाली दिल्या असता आपण असा एक गुणधर्म शोधून काढला जो कुठलीही चाल केल्यावर बदलत नाही. (उंटाच्या घराचा रंग) असे गुणधर्म शोधून काढणे हा गणितातील काही प्रश्न सोडवण्यासाठी अत्यंत चांगला डावपेच आहे.
आपल्या गाठींच्या प्रश्नाशी ह्याचे साधर्म्य आहे. तेथेही आपल्याला सर्व शक्य चाली माहित आहेत आणि आपल्याला एका गाठीहून दुसर्या गाठीकडे जाता येते का, हे पहावयाचे आहे. म्हणूनच आपण गाठींचे असे गुणधर्म शोधून काढले पाहिजेत, जे Reidemeister moves पैकी कुठलीही जरी केली, तरी बदलणार नाहीत. (आधीची गाठ आणि move केल्यानंतर झालेली गाठ ह्यांचा तो गुणधर्म सारखाच असेल.)
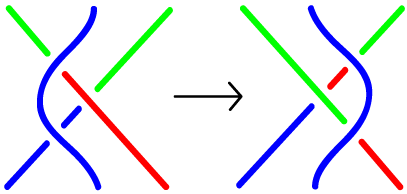
असा एक गुणधर्म म्हणजे Tricolourability. कुठल्याही गाठीला काही नियमांप्रमाणे तीन रंगांत रंगवता येते का असा हा गुणधर्म आहे. ते नियम पुढीलप्रमाणे -
(१) तीनपैकी तुम्ही २ किंवा ३ रंग वापरू शकता, पण फक्त एकच वापरलेला चालणार नाही.
(२) जेथे crossing अर्थात धागे एकमेकांवर असतील, (तेथे दोरीचे ३ तुकडे पाहता येऊ शकतात) तेथे एकत्र येणार्या तिन्ही तुकड्यांवर एकच रंग असेल, किंवा तिन्हींवर वेगवेगळा रंग असेल. (दोघांवर सारखा आणि तिसर्यावर वेगळा असे चालणार नाही.)
चित्रावरून ह्याची कल्पना जास्त येऊ शकेल.
एक Tricolourable गाठ

एक Non-Tricolourable गाठ

Tricolourability हा गुणधर्म Reidemeister moves केल्या तरी बदलत नाही. (Invariant आहे.) पुढील चित्रे बघा.
(१)
(२)
(३)
हा आपण पाहत असलेला पहिला Knot Invariant. ह्याचा वापर करून आपण Trefoil आणि Unknot सारख्या नाहीत हे अगदी सहज सांगू शकतो.
Tricoloured Trefoil
Trefoil ला वरील प्रकारे ३ रंगांत रंगवता येते, परंतु Unknot ला मात्र असे रंगवता येणार नाही. म्हणून त्या दोन्ही समान नाहीत.
अशा प्रकारे बरेच Invariants अजून आहेत. ते सारेच काही येथे सांगता येणार नाहीत. पण उदाहरण आणि प्रेरणा म्हणून या गुणधर्माकडे बघता येईल.
गुणधर्म आणि गाठींचे वर्गीकरण
वर आपण Tricolourability ह्या गुणधर्माचा वापर 'दोन गाठी समान नाहीत' हे दाखवण्यासाठी केला. परंतु अशा गुणधर्मांनी 'दोन गाठी समान आहेत' हे सांगता येईल काय? म्हणजेच, एखाद्या गाठीचे कुठले गुणधर्म माहीत असता आपल्याला ती गाठ पूर्णतः माहिती होईल? छातीठोकपणे ह्या गाठीचे आणि दुसर्या गाठीचे हे हे गुणधर्म समान असले, तर त्या गाठी स्वतःच समान आहेत हे सांगता येईल? असे प्रश्न पडतात. ह्यावर काम अजूनही चालू आहे (माझ्या माहितीप्रमाणे). गाठींचे हे गुणधर्म फक्त त्यांना एकमेकांपासून वेगळे करायला उपयोगी नसून त्यांचा भौतिकशास्त्र व इतर अनेक शाखांशीदेखील बराच संबंध आहे. त्यामुळे ते अजूनच महत्वाचे आहेत.
असे गुणधर्म कळाले की आपल्याला अगदी जीवशास्त्रात प्राण्यांचे वगैरे करतात तसे गाठींचे वर्गीकरण सुद्धा करता येऊ शकते. (ह्या गुणधर्मांची तुलना प्राण्यांच्या exoskeleton, nervous system, reproduction इत्यादींशी व्हावी.) वर बर्याच गाठींचे एक चित्र आहे. ते असेच गाठींचे त्यांच्या Crossing Number ने वर्गीकरण आहे. (Number of Crossings शी संबंधित. खरे तर हा गाठींचा सर्वात साधासुधा invariant आहे. परंतु त्याची व्याख्या करणे थोडे गुंतागुंतीचे आहे. त्याची व्याख्या कशी होईल ह्याचा विचार करून बघा.) गाठींचे असे वर्गीकरण करत राहणे हासुद्धा संशोधनाचा एक भाग आहे.
अशा रीतीने ही बरीच लांबलेली कहाणी इथेच थांबवतो. हा माझा स्वतःचा विषय नाही, त्यामुळे चुकभूल द्यावी घ्यावी. गणिताची ही एक सुंदर आणि समजण्यास तुलनेने सोपी अशी शाखा आहे. Aesthetically pleasing म्हणून ह्यातले बरेच संशोधन झाले असले तरी आता भौतिकशास्त्रात ह्याचा बराच उपयोग होतो आहे. अधिक माहितीसाठी आंतरजालावर बरीच स्थळे आहेत. तुम्हाला हे आवडल्यास जरूर अधिक माहिती मिळवा. ही तर फक्त सुरवात आहे, सितारों के आगे जहाँ और भी हैं!
(सर्व चित्रे Wikipedia / आंतर्जालावरून साभार)

भास्कराचार्य --------/\------
भास्कराचार्य --------/\------ मान गये जनाब. सुरवातीला त्याचे आप्लिकेशन्स दिले तर समजायला सोपे जाइल असे वाटते. अजुन १० वेळा तरी वाचायला लागेल हे लिहलेले समजुन घ्यायला. आता विकीवर जाउन परत येतो.
छान माहिती
छान माहिती
Interesting!
Interesting!
उच्च !
उच्च !
सगळं समजलं .काय विषय आहे आणि
सगळं समजलं .काय विषय आहे आणि नवीन अनभिज्ञांना कसे किती केवढे भरवायचे तेदेखील मराठीत हे छान जमले आहे .गोडी लागली की आणखी मागणार .गणित विषय फारच थोडयांना कळतो आणि शिकवण्याच्या क्लिष्ट पध्दतीने आणि कठीण होतो .मी कॉलेजच्या पहिल्या वर्षाला असतांना Shaum series चे set theory वरचे पुस्तक मिळाले होते .ते वाचल्यावर तो विषय फारच छान समजला होता त्याची आठवण आली .आमच्याकडे डोंबिवलीला (शंनांच्या) शेवट हलकाफुलका झाला नाहितर फाऊल धरतात .:एका नवीन जोडप्याला नासाचा निरोप आला -चंद्र यात्रेवर आठ दिवस पाठवण्यासाठी तुमची निवड झाली आहे .बायको (बहुतेक कन्या रास)उत्साहाने नवऱ्याला 'जाताना चिवडा लाडू नेऊ ,आल्यावर पिठलंभात टाकेन '
मस्त! GEB मध्ये, झेन कोआन्स,
मस्त!
GEB मध्ये, झेन कोआन्स, गाठी, आणि DNA यांची मस्त सांगड घातली आहे त्याची आठवण झाली. त्याबद्दल धन्यवाद.
आणखी लिहिणार आहात का यावर?
एका नविनच विषयाची ओळख करून
एका नविनच विषयाची ओळख करून दिल्याबद्दल प्रथमतः आभार.
वाचून काही कळतंय का ते बघते.
वाचलं. कळलंही. कोणत्याही गाठीला केवळ तीन प्रकारांनी रुपांतरीत करता येतं हा विचार अचंबित करणारा आहे.
>>> गाठींचे हे गुणधर्म फक्त त्यांना एकमेकांपासून वेगळे करायला उपयोगी नसून त्यांचा भौतिकशास्त्र व इतर अनेक शाखांशीदेखील बराच संबंध आहे. त्यामुळे ते अजूनच महत्वाचे आहेत.
>>>> कुठे उपयोगी पडतात हे जरा उदाहरणे देऊन सांगितले तर छान होईल.
छान माहिती आहे. आवडला लेख! या
छान माहिती आहे. आवडला लेख! या विषयावर आधी काही वाचल्याचे आठवत नाही. मराठीतून तर नाहीच. असे 'कन्सेप्ट्स' अजून आवडतील वाचायला.
फारएण्ड +१
फारएण्ड +१
धन्यवाद सगळ्यांना! aschig,
धन्यवाद सगळ्यांना!
aschig, त्या पुस्तकाची आठवण मलाही झालेली. अप्रतिम पुस्तक आहे ते! बाकी, ह्याविषयी अजून काही लिहीन का ते माहीत नाही. सध्या तरी याहून जास्त काही सुचत नाही प्राथमिक पातळीवरच्या लेखासाठी. तसाही हा माझा विषय नाही, त्यामुळे लेखनमर्यादा असलेलीच बरी. तुम्ही एखादा नेमका (specific) प्रश्न विचारलात तर त्याचे उत्तर द्यायचा अथवा शोधायचा प्रयत्न नक्की करेन. (ह्याच प्रतिसादात पुढे थोडे अजून लिहीतो.)
ह्यासारख्या अजून काही विषयांवर लिहिण्याचा इरादा नक्की आहे. (फारएण्ड व इतरांसाठी) जसा वे़ळ मिळेल व डोक्यात विषय रचला जाईल तसा.
शेवटी सुद्धा विनोद टाकायची कल्पना आवडली. पुढे सुचला तर नक्की टाकेन.
मामी, तो विचार खरेच अचंबित करणारा आहे. परंतु गणितात बर्याच वेळा असेच होते. Things are amazingly simple sometimes. One of the reasons to do this is to enjoy such a moment of amazement.
मामी आणि निवांत ह्यांच्यासाठी आणि सगळ्यांसाठीच, ह्याच्या उपयोगांबद्दल -
मी उपयोगांबद्दल फार काही लिहिलेले नाही कारण मी मुळात त्या invariants ची व्याख्या केलेली नाही. ती नावे द्यायला हरकत नाही, परंतु ह्यामुळे लेख क्लिष्ट वाटून लोक दूर जातील की काय असे वाटून मी ते केले नाही. माझ्या ऐकण्यात आलेला सर्वात महत्वाचा म्हणता येईल असा Invariant म्हणजे Jones Polynomial. ह्याचा Statistical Mechanics (सांख्यभौतिकी?) आणि Quantum Field Theory (पुंजभौतिकी?) ह्यांच्याशी संबंध आहे असे दिसते. गणितातल्याच इतर काही क्षेत्रांमध्ये सुद्धा ह्याचा उपयोग होतो. नक्की काय ते समजणे आणि सांगणे मात्र बरेच किचकट असावे असे वाटते. ह्यासंदर्भात प्रथमदर्शनी तरी मला दोन चांगले वाटणारे लेख -
माझ्या ऐकण्यात आलेला सर्वात महत्वाचा म्हणता येईल असा Invariant म्हणजे Jones Polynomial. ह्याचा Statistical Mechanics (सांख्यभौतिकी?) आणि Quantum Field Theory (पुंजभौतिकी?) ह्यांच्याशी संबंध आहे असे दिसते. गणितातल्याच इतर काही क्षेत्रांमध्ये सुद्धा ह्याचा उपयोग होतो. नक्की काय ते समजणे आणि सांगणे मात्र बरेच किचकट असावे असे वाटते. ह्यासंदर्भात प्रथमदर्शनी तरी मला दोन चांगले वाटणारे लेख -
http://math.berkeley.edu/~vfr/jones.pdf
http://www.ams.org/meetings/lectures/kauffman-lect.pdf
हे खूपच तांत्रिक आहेत. मलासुद्धा ते पूर्णतः कळत नाहीत. परंतु काहींना उपयोग होईल म्हणून द्यायला काही हरकत नाही. एक नोंद म्हणून.
छान माहिती. कुठे उपयोगी
छान माहिती.
कुठे उपयोगी पडतात हे जरा उदाहरणे देऊन सांगितले तर छान होईल. >>> +१
उल्झनोंका अभ्यास इतनी सुल्झाए
उल्झनोंका अभ्यास इतनी सुल्झाए तरीकेसे! मस्त.
फारएण्ड +१. अजून असे मुलभूत ज्ञानकण वाचायला आवडतील.
तुम्ही प्रतिसादात जे उपयोगांबद्दल लिहीले आहे ते मात्र काही समजले नाहीये
भार्री (अवजड) विषयावरचे
भार्री (अवजड) विषयावरचे भार्री (उच्च) लिखाण.
मराठीत असे काही लिहिल्याबद्दल अतीव आदर ---/\---
आवडला लेख. "कोणत्याही गाठीला
आवडला लेख. "कोणत्याही गाठीला केवळ तीन प्रकारांनी रुपांतरीत करता येतं" ह्यात बराच वेळ गेला करून बघताना
मस्त. सोप्या भाषेत छान
मस्त. सोप्या भाषेत छान माहिती दिलीत. अजून वाचायला आवडेल
खूप इंटरेस्टींग विषयावर मस्त
खूप इंटरेस्टींग विषयावर मस्त लिहीलं आहे आणि सोप्या भाषेत ! मला अजून बरेच वेळा वाचल्यानंतर थोडं कळण्याची आशा आहे.
पण लेख वाचून झाल्यावर मला अचानक सगळीकडे नॉट्स दिसायला लागल्या : अगदी बुटांच्या नाड्या, गिर्यारोहणाच्या नॉट्स, बोटीवरच्या नॉट्स, प्रेट्झेल, रोलर-कोस्टर, हवेत अक्षरं लिहिणारी विमानं वगैरे वगैरे!
उदाहरण नाही, पण संशोधनाचा उपयोग कुठे कुठे होतो हे समजून घ्यायला आवडेल!
एक प्रश्न: - स्प्रिंग हीसुद्धा एक प्रकारची नॉट आहे का?
मस्त भास्कराचार्य ! ह्याचा
मस्त भास्कराचार्य ! ह्याचा आणि ग्राफ प्लॅनेरिटिचा काही संबंध आहे का?
उत्तम लेख! असे अजून लेख
उत्तम लेख! असे अजून लेख आवडतील.
मस्त लेख, एका नविन विषयाची
मस्त लेख, एका नविन विषयाची ओळख करुन दिल्या बद्दल धन्यवाद!
मस्त आहे हे. आवडले.
मस्त आहे हे. आवडले.
पुन्हा एकदा धन्यवाद! तुम्हा
पुन्हा एकदा धन्यवाद! तुम्हा सगळ्यांना लिखाण आवडले आणि काहींनी खेळ करूनही बघितले हे ऐकून छान वाटले. अॅप्लिकेशन्स साठी माझा वरचा प्रतिसाद पाहा.
तुम्हा सगळ्यांना लिखाण आवडले आणि काहींनी खेळ करूनही बघितले हे ऐकून छान वाटले. अॅप्लिकेशन्स साठी माझा वरचा प्रतिसाद पाहा.
पेशवा, ग्राफ प्लेनारिटीशी याचा थोडा संबंध तरी नक्कीच लावता येईल. परंतु त्यात संशोधन कसे चालते हे मला माहीत नाही. कॉम्बिनॅटोरिअल नॉट थिअरी मध्ये हे सगळे येते. खरे तर तुमच्या प्रश्नामुळे मला एक फार सुंदर संदर्भ मिळाला, त्याबद्दल तुमचे आभार. तो हा -
तो हा -
http://homepages.math.uic.edu/~kauffman/KFI.pdf
येथे ग्राफ थिअरीशी संबंधाबद्दल बरीच माहिती आहे. पहिला exercise मस्त आहे!
दैत्य, स्प्रिंगला आपल्या व्याख्येनुसार गाठ म्हणता येणार नाही. कारण तिची दोन्ही टोके जुळलेली नसतात.
काल प्रकाशीत झालेला एक पेपर -
काल प्रकाशीत झालेला एक पेपर - नॉट्सच्या लिंकीग आणि अनलिकींग बद्दलः
https://medium.com/the-physics-arxiv-blog/2f92bda2e5fd
मस्त माहीती
मस्त माहीती
मस्त. इंटरेस्टिंग !
मस्त. इंटरेस्टिंग !
अरे, हा प्रतिसाद आत्ता पाहिला
अरे, हा प्रतिसाद आत्ता पाहिला. धन्यवाद अगो आणि जयंत.