पायथागोरसची त्रिकूटे

उपोद्घात

पायथागोरसच्या प्रमेयाबद्दल ऐकले नसेल, असे सहसा होत नाही. जवळपास प्रत्येकाने लहानपणी

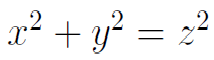
हे समीकरण पाहिलेले आहे. पायथागोरसची त्रिकूटे म्हणजे ह्या समीकरणाच्या अशा उकली, ज्यामध्ये प्रत्येक x, y, z पूर्णांक आहेत. उदा. (३, ४, ५) , (५, १२, १३) , (८, १५, १७) , (६, ८, १०) इ. ह्यांबद्दल सुद्धा आपण ऐकले असेल. अशी किती त्रिकूटे आहेत? सगळी सांगता येतील का? असा प्रश्न विचारता येऊ शकतो. आज आपण ह्याच प्रश्नाकडे बघू.

प्राथमिक माहिती

पायथागोरसचे प्रमेय खरे तर भूमितीतले विधान आहे. "कुठलाही काटकोन त्रिकोण दिला असता त्याच्या बाजूंची लांबी जर a, b, c (c हा कर्ण) असेल, तर a^2 + b^2 = c^2 हे खरे असते." आणि "उलटपक्षी, कुठल्याही ३ अशा संख्या दिल्या असता तेवढी लांबी असलेल्या बाजू घेऊन काटकोन त्रिकोण बनवता येतो." अशी दोन विधाने त्यात आहेत. परंतु, ह्यामध्ये कुठेही a, b, c तिन्ही पूर्णांक घेता येऊ शकतात अशी हमी दिलेली नाही. फक्त पायथागोरसच्या प्रमेयावरून 'तिन्ही बाजू पूर्णांक असलेले काटकोन त्रिकोण अस्तित्वात असतात का?' हे सांगता येत नाही. काही जणांचा गोंधळ यात होऊ शकतो, म्हणून मुद्दाम थोडासा इशारा.

'(a, b, c) पूर्णांक घेता येऊ शकतात का?' ह्यासारखे प्रश्न डायोफँटस ह्या ग्रीक गणितज्ञाने प्रथम विचारले असे म्हणायला हरकत नाही. त्याने हा प्रश्न पूर्णांक सहगुणक (Integer Coefficients) असलेल्या सर्वच समीकरणांसाठी मांडून तो सोडवायचा प्रयत्न केला. अशा समीकरणांना Diophantine Equations म्हटले जाते. उदा. 2x + 4y = 1, 3x^2 + 4y^2 = 5z^2, x^3 + y^3 = a^3 - b^3, Nx^2 + 1 = y^2, इ.

(येथे नमूद केले पाहिजे, की ब्रह्मगुप्त, आर्यभट, भास्कराचार्य, इ. यासारख्या भारतीय गणितज्ञांनी सुद्धा अशी काही समीकरणे पूर्णांकांमध्ये सोडवण्यात बरीच गरूडझेप घेतली होती. 'कुट्टक' व 'चक्रवाल' अशा पद्धती त्यांनी शोधून काढल्या होत्या. त्यांबद्दल पुढे कधीतरी.)

ही सर्वच समीकरणे सोडवायची एक सरसकट पद्धत अशी नाही. विशेषतः घात (power) वाढत जाईल तसे हे काम अवघड होत जाते. वरील 2x + 4y = 1, 3x^2 + 4y^2 = 5z^2 ह्या दोन्ही समीकरणांना पूर्णांकांत उकल नाही हे सांगता येते. पैकी पहिले उदाहरण अगदी सोपे आहे, दुसरे बरेच अवघड. पहिल्याचा विचार करून पाहा. (कोणी विचारल्यास मी सांगेनच.)

आपण ह्यातले फक्त x^2 + y^2 = z^2 हे पायथागोरस समीकरण आता पाहूया.

मूळ उकली (Primitive Solutions)

थोडासा विचार केल्यास लक्षात येईल, की (x, 0, x) हे कुठल्याही पूर्णांक x साठी पायथागोरसचे त्रिकूट आहे. परंतु हे म्हणजे थोडीशी पळवाट झाली. आपल्या उकलीत 0 असेल, तर तिला Trivial म्हणू. अशा Trivial गोष्टी आपल्याला नको. यापुढे फक्त non-trivial त्रिकूटे आहेत का, ह्याचाच विचार करूया.

ह्यानंतरही, प्रयत्नप्रमादपद्धतीने (Trial and Error) पायथागोरस समीकरणाची उकल सहज होते. वर म्हटल्याप्रमाणे (३, ४, ५) हे पूर्णांक ह्या समीकरणाचे समाधान करतात. त्यामुळे 'आहेत की नाहीत' ला उत्तर 'आहेत' असे सहज देता येते. ('नाहीत' असे उत्तर द्यायला जास्त कष्ट लागले असते कदाचित.)

परंतु एवढ्यावरच समाधान झाले तर अजून काय पाहिजे! ह्याच्या उकली अनंत (infinite) आहेत की सांत (finite) हे कळू शकेल का? असा प्रश्न विचारला गेला. (म्हणजेच, असे अनंत त्रिकोण शोधले जाऊ शकतात का? असा प्रश्न.) थोडा विचार केल्यावर लक्षात येते, की त्रिकोणांच्या सरूपतेने (similarity) हे सुद्धा अगदी सहज सांगता येऊ शकते. (३, ४, ५) मध्ये प्रत्येक संख्येला २ ने गुणल्यावर (६, ८, १०) हे त्रि़कूट मिळते. हा त्रिकोण आधीच्या त्रिकोणाशी सरूप आणि म्हणूनच काटकोन असणार हे उघड आहे. म्हणूनच (६, ८, १०) ही सुद्धा पायथागोरस त्रिकोणाची उकल आहे. त्याच प्रकारे ३ ने गुणून (९, १२, १५), ४ ने गुणून (१२, १६, २०) इत्यादी त्रिकूटे मिळतात. नैसर्गिक संख्या अनंत असल्याने प्रत्येकीने गुणून अशी अनंत त्रिकूटे मिळवता येऊ शकतात असे दिसते.

पण हीसुद्धा वर म्हटल्याप्रमाणे पळवाट झाली. थोडी जास्त हुषारीची, पण पळवाटच. त्यामुळे हीसुद्धा आपण बंद करून टाकूया. वरील नवीन तयार झालेल्या त्रिकूटांमध्ये तिन्ही संख्यांना १ पेक्षा मोठा सामाईक विभाजक आहे, असे दिसते. (कारण ती एकाच संख्येने गुणून बनलेली आहेत.) अशी त्रिकूटे आपण त्यांच्या पहिल्या त्रिकूटांबरोबर मोजली असे म्हणायला हरकत नाही. अशा तर्‍हेने आपण पुढील व्याख्या पाळणारी त्रिकूटेच मोजायचा प्रयत्न करूया.

व्याख्या : (a, b, c) हे जर पायथागोरसचे त्रिकूट असेल, आणि a, b, c ह्यांचा मसावि १ असेल, (जेणेकरून १ पेक्षा मोठा सामाईक विभाजक नाही) तर त्याला 'मूळ त्रिकूट' असे म्हटले जाईल. {a, b, c पैकी कुठलीही 0 नसल्याने ही व्याख्या करण्यात अडचण येत नाही.}

तर, आता आपला प्रश्न "पायथागोरसची मूळ त्रिकूटे अनंत आहेत का?" असा आहे. त्यात मी अजून थोडी भर घालतो आणि आपला प्रश्न "ती सांत असली, तर सगळी लिहा. अनंत असली तर त्यांना एखादा common form आहे का? ते सांगा." असा करतो. म्हणजेच "एखादा फॉर्म्युला आहे का, ज्याने ती सर्व निर्माण करता येतील?" (सांत किंवा अनंत)

टीपः अशा फॉर्म्युल्याची अपेक्षा करणे अवाजवी वाटेल, परंतु बर्‍याच वेळा तसा तो असतो. किंबहुना, इथूनच त्याची सुरवात झाली असे म्हणता येईल.

वक्रांवरील बिंदू (Points on Curves)

ही आजची Technique आहे. मी वरील समीकरणाच्या उकलींची आता एका वेगळ्याच भौमितीक प्रश्नाशी सांगड घालतो.

हे XY-प्रतलातील वर्तुळाचे समीकरण आहे हे बहुतेकांना माहीत असेल. {केंद्रबिंदू (0, 0)}

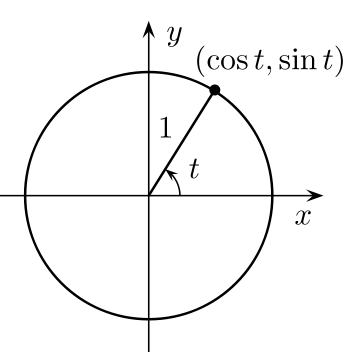
ह्या समीकरणाचा आणि आपल्या पायथागोरस समीकरणाचा संबंध लावता येतो. पायथागोरस समीकरणात z^2 ने दोन्ही बाजूंस छेद दिल्यास (आपण z हा 0 नाही अश्या उकली बघणार असल्याने ह्याने फरक पडणार नाही.) आपल्याला (x/z)^2 + (y/z)^2 = 1 असे येते.

म्हणजेच, (a, b, c) ही पायथागोरस समीकरणाची उकल जर असेल, तर त्याचा संबंध (correspondence) वर्तुळावरच्या (a/c , b/c) ह्या बिंदूशी लावता येतो. उलटपक्षी, जर (p/r , q/r) हा जर वर्तुळावरील बिंदू असेल, तर त्याचा संबंध छेद नाहीसे केल्यानंतर तयार होणार्‍या (p, q, r) ह्या उकलीशी लावता येतो.

जर (a, b, c) हे तिन्ही पूर्णांक असतील तर? तर वर्तुळावरच्या संबंधित बिंदूचे को-ऑर्डिनेट्स हे परिमेय (rational) असतात. अशा बिंदूंना 'परिमेय बिंदू' (rational points) म्हणू. त्याच प्रकारे, वर्तुळावरचा असा बिंदू मिळाल्यास संबंधित त्रिकूटातील तिन्ही संख्या पूर्णांक असतील. तसेच, आपल्याला लक्षात येईल, की एकाच मूळ त्रिकूटाला गुणून जी त्रिकूटे येतात, ती (आणि ते मूळ त्रिकूट) सर्व वर्तुळावरील एकाच बिंदूशी संबंधित असतात. ह्याचाच अर्थ, जर वर्तुळावरील सर्व परिमेय बिंदू सांगण्याचा एखादा मार्ग जर मिळाला, तर सर्व मूळ त्रिकूटे सांगता येतील.

हीच पद्धत गणितात फार महत्वाची आहे. (Counting Rational Points on Curves) ह्याचा एक वेगळाच उपयोग नंतर निदर्शनास आला. त्याविषयी थोडक्यात लेखाच्या शेवटी लिहितो.

[येथून पुढचा भाग थोडा जास्त तांत्रिक आहे, त्याबद्दल क्षमस्व. परंतु ज्यांना १२वीपर्यंत गणित होते, अशांना थोडा प्रयत्न करून वाचता यायला हरकत नाही असे मला वाटते. न कळल्यास सरळ शेवटचा फॉर्म्युला बघितल्यास हरकत नाही.)

वर्तुळावरील परिमेय बिंदू (Rational Points on the Circle)

आपण आपला प्रश्न रूपांतरित केला खरा, पण त्याचा काही फायदा आहे काय? असा विचार मनात येऊ शकतो. एका कठीण प्रश्नाचा आपण दुसरा तेवढाच कठीण प्रश्न बनवला नाही ह्याची काय खात्री? परंतु ह्या बाबतीत आता आपण भूमितीच्या कल्पना वापरून अतिशय सुंदररीत्या उत्तराप्रती पोहोचू शकतो. (मागे एका लेखात मी म्हटले होते, की एकीकडची tools वापरून दुसरीकडचे न सुटणारे प्रश्न सोडवता येऊ शकतात.) ते पुढीलप्रमाणे -

(1, 0) हा बिंदू वर्तुळावर आहे हे अगदी सहज दिसते. हा बिंदू आपल्याला नको, कारण तो trivial त्रिकूटाशी संबंधित आहे. परंतु ह्याचा वापर करून आपण नवीन बिंदू तयार करूया.

(1, 0) मधून जाणारी, slope = -t असलेली सरळ रेषा (-t निवडायचे कारण काही खास नाही. फॉर्म्युला चांगला दिसावा म्हणून उगाच.)

ही आहे. ही रेषा वर्तुळाला दोन बिंदूंमध्ये छेदते. पैकी एक (1, 0) हा आहे. दुसरा बिंदू आपल्याला या रेषेचे समीकरण वर्तुळात substitute करून मिळेल.

मध्ये घातले, की येते -

हे समीकरण Quadratic Equation आहे. हे अगदी सहज सोडवता येते. त्यातून आपल्याला दुसर्‍या बिंदूचा X co-ordinate मिळतो. तो आहे -

तो रेषेच्या समीकरणात वापरून आपल्याला Y co-ordinate सुद्धा मिळतो. तो असा -

ह्यावरून आपल्याला त्रिकूटासाठी पुढील फॉर्म्युला मिळतो -

उलटपक्षी, जर का कुठला परिमेय बिंदू वर्तुळावर असेल, तर त्याला आणि (1 , 0) ला जोडणार्‍या रेषेचा slope, हा slope च्या व्याख्येमुळे, परिमेय (m/n) असतो आणि मग त्या बिंदूचे co-ordinates वरील फॉर्म्युल्यातच बसतात.

आणि म्हणूनच, वरील फॉर्म्युला पायथागोरसची सर्व मूळ त्रिकूटे (खरे तर सगळीच त्रिकूटे) देतो असे आपण दाखवून दिलेले आहे.

उपयोग

पायथागोरसच्या प्रश्नामुळे आपली 'परिमेय बिंदू मोजणे' ह्या पद्धतीशी ओळख झाली. वर्तुळासारख्या 'चांगल्या' वक्राच्या (curve) बाबतीत एका परिमेय बिंदूपासून इतर सर्व बिंदू मिळवता येतात. (कारण रेषा ज्या दुसर्‍या बिंदूमध्ये छेदते, तोसुद्धा परिमेय निघतो.) परंतु इतर बाबतीत हे काम इतके सोपे नाही. सर्वसाधारणपणे वक्रावरील बिंदू शोधणे अवघड असते. दोन बिंदू दिले असता त्यांचे एकमेकांशी नाते शोधणेही अवघड असते. ह्या अवघडपणाचा वापर Computer Security मध्ये केला जातो. (Elliptic Curve Cryptography सर्च करून पहा.) त्याबद्दल पुन्हा कधीतरी लेख लिहिण्याचा प्रयत्न करेन. पूर्णांकांशी संबंधित एका साध्याशा प्रश्नातून अशी छान पद्धत निर्माण झाली हेच आश्चर्यकारक आहे.

(वरील चित्र विकीपीडिया वरून साभार.)