सर्कस आकड्यांची

[हा संपूर्ण लेख जशी डोक्यात विचारांची साखळी येत गेली तसाच उतरवला आहे. म्हणून तो तुटक किंवा उड्या मारत लिहिला गेलाय असे वाटण्याची खूपच शक्यता आहे. अगदी प्रामाणिकपणे सांगायचे झाले तर तुम्ही हा लेख एका झटक्यात पूर्ण वाचणे अपेक्षित नाही... किंवा कधीच पूर्ण वाचणे अपेक्षित नाही असे म्हटले तरी चालेल हा लेख वाचताना कुठल्याही क्षणी तुम्हाला स्वतःला त्या संदर्भात काही गुगलावेसे वाटले, कुठलीतरी गणिती संकल्पना अधिक जाणून घ्यावीशी वाटली आणि तुम्ही हा लेख मध्येच सोडून तिकडे गेलात आणि तिकडे त्या गणिताबद्दल/संकल्पनेबद्दल वाचताना आणखी काहीतरी 'इंटरेस्टिंग' वाटले आणि आणखी तिसरीकडेच गेलात तर फारच उत्तम! या अर्थाने हा लेख तुमच्यासाठी पंचतंत्रातील गोष्टींसारखा ठरणे हेच या लेखाचे उद्दिष्ट होय.

या लेखाची भाषा अगदी लहान मुलांना समजावून सांगितल्यासारखी वाटणे स्वाभाविक आहे. परंतु, यात वाचकांचा उपमर्द करण्याची इच्छा मुळीच नाही. हा लेख म्हणजे मी जे व ज्या प्रकारे माझ्या पोरांना सांगतो ते उतरवले गेले आहे. त्यात वाचकांच्या समजुतीला/ज्ञानाला/शिक्षणाला कमी लेखण्याचा मुळीच उद्देश नाही. व्यवसायामुळे काही गोष्टी अंगी इतक्या (नको इतक्या) भिनल्यामुळे ही भाषा आपोआप येते व त्याबद्दल मी आधीच वाचकांची क्षमा मागतो.

हा लेख वाचलात अथवा न वाचताही याउप्पर तुमच्याकडील खजिना इथे उघडलात तर सोन्याहून पिवळे! ]

आज चित्रा यांच्या 'गणितातील रूल बदलले आहेत का?' या प्रश्नावर जी चर्चा झाली त्यातून डोक्यात विचारांची आगगाडी सुरू झाली. आपण शाळेत शिकलेले गणित, मग विद्यालयीन, मग पदव्युत्तर शिक्षणादरम्यान शिकण्याचा प्रयत्न केले गणित अश्या वेगवेगळ्या पातळ्या डोळ्यांसमोर उभ्या राहिल्या. पण त्या सगळ्यांत सर्वात ठळक गोष्ट वाटली ती म्हणजे गणितातील शिकलेल्या किंवा कळलेल्या गंमतीजमती. 'डबल इंटिग्रेशन', 'ट्रिपल इंटिग्रेशन', 'पार्शल डिफरन्शिअल इक्वेशन्स' वगैरे भरीच्या गोष्टी एकीकडे आणि '२, ०, ३, ५, ७ यांपासून सहा आकडी लघुत्तम संख्या बनवा' यासारखे भारीचे प्रश्न दुसरीकडे. त्या भरीच्या गोष्टी नंतर कधीतरी कराव्याश्या वाटल्या कारण आधी कधीतरी या भारीच्या गोष्टी करताना मजा आली होती म्हणूनच. किंबहुना, त्या करताना गंमत आली म्हणून तर त्या भारीच्या. व्यवसायाच्या निमित्ताने परत जेव्हा या शालेय/महाविद्यालयीन गणिताकडे वळलो तेव्हा परत त्याच मजेचा शोध सुरू झाला.

गणित म्हणजे शेवटी आकड्यांचीच सर्कस. हे आकडे, संख्या अगदी सर्कशीतल्या कलाकारांसारखेच उलटेसुलटे होणारे, 'इकडून' झेपावून बघता बघता 'तिकडे' जाणारे, कुठल्यातरी रेषेला लोंबकळत असलेले आणि वरून कुठूनतरी कोसळताना मध्येच अचानक एकत्र येऊन काहीतरी अकल्पित सुंदर रचना करणारे... तर कधी त्या विदूषकांसारखे, एकाच्या पोटातून बाहेर येणारे दुसरे आकडे, एकाच्या अंगावर बदाबदा पडणारे आकडे, सरळ चाललेत असे वाटता वाटता घसरून नाहीसे होणारे, बुटके आकडे, लंबू आकडे... एक ना दोन. अरेच्चा! परत भाषेतही आकडेच. मग यात आले सम संख्या (इव्हन नंबर्स), विषम संख्या (ऑड नंबर्स), मूळ संख्या (प्राइम नंबर्स), संयुक्त संख्या (कम्पोझिट नंबर्स), परिपूर्ण संख्या (परफेक्ट नंबर्स), रॅशनल, इररॅशनल, रिअल, कॉम्प्लेक्स.... ढीगभर संख्या आणि त्यांचे ढीगभर प्रकार! पण हे ढीगभर असल्याने ढीगभर मजासुद्धा आहे. पायचेच घ्या.

पाय ही फार शाही खानदानी संख्या. प्रत्येक वर्तुळाचा परीघ आणि व्यास यांचे गुणोत्तर (म्हणजेच परीघ भागिले व्यास हो सोप्या शब्दांत). यांतला सर्वात महत्त्वाचा शब्द 'प्रत्येक'. अगदी कुठलेही वर्तुळ घ्या, पार अणूच्या आकाराचे अथवा पृथ्वीच्या आकाराचे... भागाकार तोच. आपण शिकलो पाय = २२/७ किंवा ३.१४. पण ही संख्या पडली इर-रॅशनल (irrational), म्हणजेच ती कुठल्याही दोन संख्यांच्या भागाकाराने अचूक दाखवणे शक्यच नाही. मग २२/७ कुठून आले? तर आपल्या नेहमीच्या व्यवहारात/गणितात पाय या पूर्ण संख्येचा ३.१४ एवढाच भाग घेतला तरी पुरेसे अचूक उत्तर मिळते. हे 'पुरेसे अचूक' काय भानगड आहे? हा प्रश्न पडलाच असेल. अचूक हे अचूक असते नाहीतर चूक असते. पुरेसे अचूक म्हणजे तुम्हाला किती चूक पाहिजे? खूप चूक चालत असेल तर फक्त ३ घ्या, कमी चूक (= जास्त अचूक) पाहिजे असेल तर ३.१४ घ्या, याहूनही कमी चूक पाहिजे असेल तर... तर मात्र २२/७ चालणार नाही, कारण २२/७ चे उत्तर येते ३.१४२८५७.... आणि पायचे मूल्य तर आहे ३.१४१५९.... मग हे कुठून आणायचे? तर ३५५/११३ = ३.१४१५९.... हां, चला, म्हणजे ३.१४ पेक्षा कमी चूक उत्तर मिळण्याची सोय तर झाली. पण हे लक्षात कसे ठेवायचे? २२/७ किंवा ३.१४ लहानपणापासून वापरल्यामुळे डोक्यात फिट्ट बसले आहे. तर त्यासाठी एक पाककृती/स्मृतीपाठ (mnemonic) आहे -
पहिल्या तीन विषम संख्या घ्या. १, ३, ५.
त्या प्रत्येकी दोनवेळा शेजारीशेजारी लिहा. ११३३५५.
एकूण सहा आकडे मिळाले. त्यांची बरोबर दोन समान संघांत विभागणी करा. ११३ ३५५.
मोठा तो वर, छोटा तो खाली. ३५५/११३. झाले. मिळाला पाय ३.१४ पेक्षा जास्त अचूक.
आणखी एक. पायचा वर्ग केलात तर काय मिळते ठाऊक आहे? जवळजवळ आपला १०. साधा सरळ १०. अगदी अचूकपणे १० नाही, पण पायचा वर्ग = पाय x पाय = ९.८६९६ म्हणजे १० च म्हणा की. तर पायकडे जाण्याचा आणखी एक मार्ग मिळाला -
पाय = १० चे वर्गमूळ.
हवेत सोडलेली/टाकलेली प्रत्येक गोष्ट जमिनीवरच येते. हळूहळू येत नाही ना? तिचा वेग तर वाढत जातो. म्हणजे दुसर्‍या मजल्यावरून चेंडू खाली टाकला, तर जमिनीवर येईपर्यंत त्याचा वेग वाढलेला असतो. याचे कारण गुरूत्वाकर्षण. तर हा वेग वाढण्याचासुद्धा वेग असतो. वेग वाढण्याचा वेग म्हणजेच अ‍ॅक्सीलरेशन (त्वरण). पृथ्वीचे गुरूत्वीय त्वरण (ग्रॅव्हिटेशनल अ‍ॅक्सिलरेशन) किती आहे? साधारणपणे ९.८ मीटर प्रति सेकंद प्रति सेकंद (हा टायपो नाही!). म्हणजे जवळजवळ १० च परत! हे तर अजूनच छान. म्हणजे -
पाय = पृथ्वीच्या ग्रॅव्हिटेशनल अ‍ॅक्सिलरेशनचे वर्गमूळ
(हा जंगी पाय, आपला १० ज्यावर आपली संख्याव्यवस्था उभारली आहे आणि पृथ्वीचे गुरूत्वीय त्वरण या तीन पूर्ण विभिन्न गोष्टींचा असा अचाट संबंध पाहून अनेक लोकांना वाटते की हा नक्कीच योगायोग नाही. ही देवाची/अमानवीय शक्तीची/शक्तीमान मुकेश खन्नाची करणी आहे. पण तसे काही नाही. असल्या लोकांच्या नादी लागण्यापेक्षा आपण पुढे जाऊ.)
पण काही जण म्हणतील ते सगळे ठीक आहे. त्याशिवाय दुसरे काही नाही का? तर आहे ना. खालील कविता लक्षात ठेवायची -

साइन कॉस टॅन, टॅन कॉस साइन
थ्री पॉइंट वन फोर वन फाइव्ह नाइन

चाल लावा. गुणगुणा. मोठ्याने गा. गणपती बाप्पा मोरयासारखे ओरडा किंवा खास अमेरिकन जनतेसाठी, तुमच्या संघाच्या चीअरच्या तालात म्हणा.
पण काही चिवट लोक विचारतील, याहीपेक्षा अचूकता माझ्या उत्तरात पाहिजे असेल तर? मला हे तुमचे ३.१४१५९ सुद्धा पुरेसे बरोबर वाटत नाही. मला आणखी आकडे पाहिजेत. जरूर मिळतील. हे घ्या -

(१/१) - (१/३) + (१/५) - (१/७) + (१/९) - (१/११) + (१/१३) - (१/१५) + ......

अशी बेरीज करत रहा पार अनंतापर्यंत. हिला म्हणूया अनंतबेरीज (इन्फायनाइट सम). या संख्यांची संरचना लक्षात येतीये ना? आकडे कसे निवडलेत, कसे ठेवलेत? (+) व (-) यांना कसे आलटून पालटून वापरले आहे? तर ते लक्षात घेऊ, म्हणजे आपल्याला या बेरजेतील पाहिजे तितक्या पुढच्या संख्या लिहिता येतील. ही बेरीज येते अगदी बरोबर पाय/४. म्हणजेच -

पाय = ४ x [(१/१) - (१/३) + (१/५) - (१/७) + (१/९) - (१/११) + (१/१३) - (१/१५) + ...... ]

आता आपल्याकडे चावीच आली पायची. जितके जास्त अचूक उत्तर पाहिजे तितक्या जास्त संख्या बेरजेत लिहायच्या आणि बेरीज करायची.

पण आता दुसरेच काहीतरी उभे राहिले. हे साइन, कॉस, टॅन प्रकरण. त्रिकोणाशी संबंधित काहीतरी आहे, त्रिकोणातील कोनांशी संबंधित काहीतरी आहे. बरोबर. पण आज थोडी वेगळी ओळख. त्यांचा संबंध खरंतर त्या कोनांशी अथवा त्रिकोणांपेक्षाही मूळचा दुसरीकडे कुठेतरी लागतो. ही सगळी मंडळी वेगवेगळ्या प्रकारच्या अनंतबेरजा आहेत. पण आता कोनाचा विचार अंशांमध्ये करायचा नाही. कोनांचा विचार करायचा 'रेडियनां'मध्ये. म्हणजे आपण मोजतोय कोनच, पण अंशांच्या ऐवजी रेडियनांमध्ये. म्हणजे भारतात अंतर मोजतात किलोमीटरांमध्ये, पण अमेरिकेत मैलांमध्ये. तसं गणिताला अंश कळतच नाहीत. म्हणून गणितात कोन मोजायचा रेडियनांमध्ये. हे रेडिअन कसे घ्यायचे? तर परत आला आपला पाय!

१ अंशाचा कोन = (पाय/१८०) रेडिअनचा कोन.
मग ३० अंश = पाय/६ रेडिअन, ९० अंश = पाय/२ रेडिअन इ.इ.

आता आणखी एक गोष्ट. ४! म्हणजे चार आकडा प्रचंड आश्चर्याने किंवा प्रचंड आनंदाने किंवा वैतागाने म्हणायचा नाही. (गणितद्वेषी मंडळींनी मात्र करायला हरकत नाही. थोडे बरे वाटेल.) याचा उच्चार करायचा 'फोर फॅक्टोरिअल' असा आणि अर्थ घ्यायचा असा -

४! = ४ x ३ x २ x १
तसेच इलेव्हन फॅक्टोरिअल म्हणजे
११! = ११ x १० x ९ x ८ x ७ x ६ x ५ x ४ x ३ x २ x १

आता आपल्याला त्या उद्गारवाचकचिन्हाचा अर्थ कळला. थोडक्यात काय, तर ते चिन्ह म्हणजे एवढा सगळा गुणाकार लिहिण्यासाठीचा शॉर्टकट. मग आपण त्या साइन, कॉस मंडळींकडे नव्या नजरेने बघायला तयार झालो. लक्षात ठेवू की या अनंतबेरजा आहेत आणि यातला एक्स म्हणजे कोन पण रेडिअनमधला.
फिर चलो -

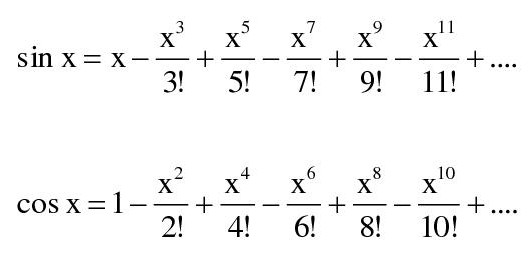
इथे एका मोठ्या प्रश्नाचे उत्तर मिळते. साइन, कॉस वगैरे जर फक्त त्रिकोणातील कोनांशी संबंधित असतील तर साइन (२०० अंश) म्हणजेच २०० अंशाच्या साइनचे मूल्य कसे काढणार? त्रिकोणातील कुठलाच कोन १८० अंशापेक्षा जास्त नसतोच. तर आता कळते की २०० अंशाला रेडिअनमध्ये बदलायचे. वरच्या साइनच्या अनंतबेरजेत एक्सच्या जागी हा आकडा घालायचा की मिळाले आपल्याला २०० अंशाच्या साइनचे मूल्य.

अनंतबेरजा पाहिल्या की आणखी एका अनंतबेरजेची आठवण येते. ती दिसायला एकदम दडपून टाकणारी आहे खरी, पण दा विन्ची कोड वाचकांना ओळखीची असेल. तोच सुप्रसिद्ध 'गोल्डन रेशो'. तो गोल्डन रेशो असल्याच एका अनंतबेरजेद्वारे दाखवता येतो -

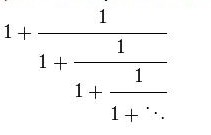
याचे मूल्य आहे १.६१८.... (हासुद्धा 'पाय'सारखा न संपणारा). बाकी याची महती 'दा विन्ची कोड'मुळे आपल्याला कळली आहेच, नाहीतर गुगल आहेच. तो कसा निसर्गातच अनपेक्षित ठिकाणी आढळतो इ. इ. पण आपण गणितापुरतेच बघू. खालचा पंचकोन बघा. हा नियमित म्हणजे रेग्युलर आहे. म्हणजेच त्याची प्रत्येक बाजू समान लांबीची आहे. असा एक पंचकोन तयार करू ज्याची प्रत्येक बाजू नुसती समानच नाही तर बरोबर 'एक' लांबीची आहे. म्हणजे १ सेंमी किंवा १ मिलिमीटर किंवा १ किलोमीटारसुद्धा चालेल, फक्त जे काय घ्यायचे ते '१' एवढेच घ्यायचे.
AB = BC = CD = DE = EA = 1 (समजा, सेंटिमीटर.)

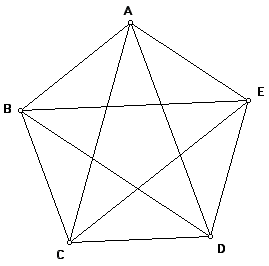
असा पंचकोन तयार केला की त्याचे सर्व कोपरे एकमेकांशी जोडा. तर आत एक तारा तयार होईल. आता या तार्‍याची प्रत्येक बाजूची लांबी बरोबर 'गोल्डन रेशो' एवढी भरते. तार्‍याची प्रत्येक बाजू = १.६१८.... सेंमी!

म्हणजे हे आकडे नुसते एकमेकांबरोबरच खेळत नाहीत, तर चित्रांशीसुद्धा खेळतात. फक्त इथे घ्यायची गणिती चित्रे... म्हणजे आपली 'भूमिती' हो! आपला भूमितीशी आता फारसा संबंध उरला नसला तरी काही गोष्टी मात्र पक्क्या लक्षात असतात. म्हणजे वर्तुळ, व्यास, त्रिज्या, पाय इ. तसेच काटकोन त्रिकोण आणि काटकोन त्रिकोणाबरोबर अपरिहार्यपणे येणारा पायथागोरस आणि त्याचा तो जगप्रसिद्ध सिद्धांत -

(काटकोन त्रिकोणाच्या एका बाजूच्या लांबीचा वर्ग) + (काटकोन त्रिकोणाच्या दुसर्‍या बाजूच्या लांबीचा वर्ग) =
(काटकोन त्रिकोणाच्या कर्णाचा वर्ग)
(square of one side of a right triangle) + (square of the other side of the right triangle) =
(square of the hypotenuse)

हा सिद्ध (प्रूव्ह) करण्याचे शेकडो मार्ग आहेत. आपण त्यातील एक खास मार्ग बघू. एक कुठलाही काटकोन त्रिकोण तयार करू. त्याच्या बाजू असतील a, b आणि c. आपल्याला सिद्ध करायचे आहे -
a^2 + b^2 = c^2

आता खालील चित्र पाहू. त्यात असाच एक पिवळा काटकोन त्रिकोण ठेवलाय. मग त्याच्याच एका टोकाला जुळवून तसाच एक त्रिकोण ठेवला - निळा. पण पिवळा आणि निळा अगदी सारखेच आहेत. आता या पिवळ्या-निळ्या त्रिकोणांची वरची दोन टोके जुळवून टाकू. म्हणजे आपल्याला आणखी एक त्रिकोण मिळेल - गुलाबी (हा रंग मला तरी गुलाबी या नावानेच ओळखता येतो, त्याचे नाव aurora pink किंवा egyptian pink असल्यापैकी असेल किंवा तो गुलाबीच नसेल तर क्षमस्व! गुलाबी = पिवळा व निळा सोडून जो असेल तो.).

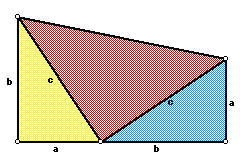
हे तिन्ही त्रिकोण मिळून एक विशिष्ट चौकोन तयार झालाय, त्याला म्हणतात 'ट्रपिझिअम' (trapezium) किंवा 'ट्रपिझॉइड' (trapezoid). यात दोन सरळसोट उभ्या बाजू एकमेकांना समांतर आहेत. अश्या प्रकारच्या चौकोनांचे क्षेत्रफळ (area) काढण्यासाठी पुढील सूत्र वापरतात -

असल्या चौकोनांचे क्षेत्रफळ = (समांतर बाजूंच्या बेरजेचा वर्ग) / २
area of a parallel trapezium = (square of the sum of parallel sides) / 2

तेव्हा या सूत्रानुसार,
वरील चौकोनाचे क्षेत्रफळ = A =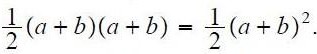

पण हा चौकोन या तीन त्रिकोणांपासून बनला आहे, त्यामुळे
चौकोनाचे क्षेत्रफळ = तीन त्रिकोणांच्या क्षेत्रफळांची बेरीज.

शिवाय, त्रिकोणाचे क्षेत्रफळ = (तळाकडाची बाजू x त्रिकोणाची उंची) / २
area of a triangle = (base x height) / 2

त्यामुळे,
पिवळ्या त्रिकोणाचे क्षेत्रफळ = निळ्या त्रिकोणाचे क्षेत्रफळ = ab / 2
गुलाबी त्रिकोणाचे क्षेत्रफळ = cc/2 = (c^2)/2

आता, (तीन त्रिकोणांच्या क्षेत्रफळांची बेरीज = चौकोनाचे क्षेत्रफळ) हे वापरू या -

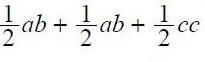
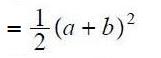
आता दोन्ही बाजूंना २ ने गुणून आपल्याला मिळेल (इथे फक्त वरच्या समीकरणातील डाव्या-उजव्या बाजूंची अदलाबदल केलीये एवढेच) -

मग डाव्या बाजूचा विस्तार करून पुढच्या पायर्‍या -

अश्या प्रकारे आपण पायथागोरसचा सिद्धांत सिद्ध केला. पण उपलब्ध असलेल्या शेकडो मार्गांपैकी आपण हाच मार्ग का निवडला या प्रश्नाचे उत्तर रोचक आहे. पायथागोरसाच्या सुप्रसिद्ध सिद्धांताची ही सिद्धता (= प्रूफ) शोधून काढणारा माणूसही कालांतराने सुप्रसिद्ध झाला, पण अगदी वेगळ्याच क्षेत्रात... हा हुषार गणिती म्हणजे जेम्स गारफील्ड, अमेरिकेचा २०वा राष्ट्राध्यक्ष!

या सिद्धांताचा जनक, पायथागोरस, स्वत: एक अवलियाच होता. त्याची ती गुप्त संघटना - 'पायथागोरिअन ब्रदरहूड', त्याचे 'परिपूर्ण' आकड्यांबद्दलचे आणि एकंदरीतच आकड्यांवरचे अफाट अफाट प्रेम, त्याने व त्याच्या शिष्यांनी गणिताला आणि म्हणूनच संपूर्ण मानवजातीला दिलेले योगदान हे सर्व एका वेगळ्याच लेखाचा विषय होतील. ते नंतर कधीतरी. पण सध्या ऑलिंपिक सुरू आहे. तेव्हा या लेखाचा शेवट पायथागोरस आणि ऑलिंपिक यांना जोडणार्‍या दुव्याने करणे उचित ठरेल.
असे मानतात की 'फिलॉसॉफर' या शब्दाचा जन्मदाता पायथागोरसच. त्यानेच हा शब्द प्रचलित केला. एका वर्षीच्या ऑलिंपिकला हजर असताना पायथागोरसने राजपुत्र लिऑनशी बोलताना स्वतःला उद्देशून 'फिलॉसॉफर' असा शब्दप्रयोग केला. लिऑनने हा शब्दप्रयोग कधीच ऐकला नसल्याने त्याने पायथागोरसला या शब्दाचा अर्थ विचारला. तेव्हा पायथागोरस त्याला म्हणाला होता[१], "Life, Prince Leon, may well be compared with these public Games for in the vast crowd assembled here some are attracted by the acquisition of gain, others are led on by the hopes and ambitions of fame and glory. But among them there are a few who have come to observe and to understand all that passes here.
It is the same with life. Some are influenced by the love of wealth while others are blindly led on by the mad fever for power and domination, but the finest type of man gives himself up to discovering the meaning and purpose of life itself. He seeks to uncover the secrets of nature. This is the man I call a philosopher for although no man is completely wise in all respects, he can love wisdom as the key to nature’s secrets."
आमेन!
***

[१] Fermat's Enigma: The Epic Quest to Solve the World's Greatest Mathematical Problem - Simon Singh.
सर्व चित्रे आंतरजालावरून साभार.