चातुर्वर्गांची समस्या

मंडळी, धाग्याचं शीर्षक वाचून तुम्ही कदाचित वेगळ्याच अपेक्षेने हा धागा उघडला असेल. कदाचित 'मायबोलीवर ह्या विषयावर अजून एक धागा आला की काय' असंही तुम्हाला वाटलं असेल. पण ह्या धाग्याचा विषय वेगळाच आहे! हा धागा वेगळ्याच 'वर्ग'वारीमध्ये मोडतो. आता इथवर आलाच आहात, तर मागे न वळता चला माझ्याबरोबर पुढे. एकदा बघू तरी काय प्रकार आहे हा.

नैसर्गिक संख्या आणि वर्गसंख्या - गुणोत्तर/घनता किती?

पूर्णवर्गसंख्यांशी आपण शाळेपासून परिचित आहोत. ' नैसर्गिक संख्येचा वर्ग म्हणजे त्या नैसर्गिक संख्येचा त्याच संख्येशी गुणाकार करून येणारी संख्या' अशी व्याख्या सगळ्यांनीच कधी ना कधी घोकलेली आहे.

अश्या वर्गसंख्या तुम्ही पाठही केल्या असतील. (अगदी इतक्या नसल्या, तरी ह्यातल्या काही नक्कीच केल्या असतील.) ह्या तक्त्याकडे पाहिल्यावर लक्षात येईल, की पहिल्या १०० संख्यांमध्ये १०च संख्या पूर्णवर्गसंख्या आहेत, तर पहिल्या ३६०० संख्यांमध्ये ६०च संख्या पूर्णवर्ग आहेत. म्हणजे संख्या ३६ पट झाल्या, तर पूर्णवर्ग मात्र ६ पटीनेच वाढले. ह्यावरून सहज लक्षात येते, की संख्या जसजशा वाढत जातात, तसतशी त्यांच्यातल्या पूर्णवर्गसंख्यांची संख्या विरळ होत जाते. आता हेच पहा ना. १ ते १० ह्या संख्यांमध्ये १, ४, ९ अश्या चांगल्या तीन वर्गसंख्या आहेत, पण ५१ ते ६० ह्या संख्यांमध्ये एकही वर्गसंख्या नाही. अश्या रीतीने पूर्णवर्गसंख्या सर्व नैसर्गिक संख्यांच्या तुलनेत कमी कमी होत जातात, हे छोटेसे पण महत्वाचे निरीक्षण आहे. जशी वायूची घनता असते, तशी ह्या वर्गांची सुद्धा घनता असते, आणि आकारमान वाढत गेल्यावर ती विरळ होत जाते, असंच म्हटलं पाहिजे की!

पूर्णवर्गांची बेरीज करूया!

पण गणितवाले लोक काही अश्या निरीक्षणांवर स्वस्थ बसत नाहीत बघा. वर्ग कमी होतायत ना? होऊ दे. पण आपण फक्त एका पूर्णवर्गसंख्येकडे का बघायचं? आपण दोघांची, नाहीतर तिघांची, अशी बेरीज करून कुठल्या संख्या तयार होतात, ते बघू, असे प्रश्न त्यांना पडायला लागतात. मग ते अजून नवनवीन संख्या तयार करतात.

अश्या आपल्याला अजून काही संख्या मिळाल्या. पण असं करून सगळ्याच संख्या मिळतात का? तर अर्थातच नाही. ३ = १ + १ + १ अशीच फोड होऊ शकते. ६ ही संख्या दोन पूर्णवर्गांची बेरीज म्हणून लिहिता येत नाही, हे सहज दिसते. तिला तीन पूर्णवर्गच लागतात.

६ = ४ + १ + १, ११ = ९ + १ + १, १४ = ९ + ४ + १

अश्या अजून संख्या आपल्याला तीन पूर्णवर्ग वापरून लिहिता येतात. पण ह्यांनीसुद्धा सगळ्या संख्या नाही लिहिता येत.

७ = ४ + १ + १ + १ असंच लिहावं लागतं. चारपेक्षा कमी पूर्णवर्ग चालणार नाहीत, हेही सहज लक्षात येते.

मग 'आता हे मारुतीच्या शेपटासारखं सोंग वाढतच जाणार की काय?' असं वाटणं साहजिक आहे. दरवेळेस वर्गांची संख्या एकाने वाढवली, की नवीनच एक संख्या 'पुरणार नाही!' असं म्हणत दत्त म्हणून समोर येऊन राहतेय की! वर्गसंख्या विरळ होत जातात, हे आपण पाहिलंच आहे. त्यामुळे असं वाटणंही योग्यच आहे, की बुवा संख्या जसजशी मोठी होत जाईल, तसतशी तिची वर्गांमध्ये फोड करायला जास्तजास्त तुकडे लागत राहतील. कारण बेरीज करायची आहे म्हणजे वर्ग संख्येपेक्षा छोटेच हवेत, आणि ते तर विरळ विरळ होत जातायत.

पण, (हा 'पण' नेहमी असतोच.) काहीतरी अक्षरशः जादू होते ह्या '४' विषयी. आपण अशी संख्या शोधायला जावं, की जिला पाचपेक्षा कमी वर्ग लागूच शकत नाहीत, आणि ती मिळूच नये, असं होतं! प्रयत्न करून बघा.

३१ = २५ + ४ + १ + १,
११२ = ६४ + १६ + १६ + १६,
१२७ = १२१ + ४ + १ + १,

अश्या तीन पूर्णवर्ग न पुरणार्‍या सर्वच संख्या अचानक चार पूर्णवर्गांमध्ये फोडून लिहिता येतात! म्हणजे पूर्णवर्ग विरळ होत असले, तरी चारच पूर्णवर्ग संख्यांची बेरीज करून सगळ्याच संख्या लिहिता येतात की काय! हे विधान जर खरंच बरोबर असेल, तर ते आपल्याला नैसर्गिक संख्यांमध्ये दडलेल्या आकृतीबंधांविषयी काहीतरी मोलाचे सांगते आहे, हे लक्षात घ्या. नंबर थिअरीस्ट्स हे असे गुणधर्म शोधण्याचा प्रयत्न करतात, आणि म्हणूनच ते अश्या विधानांच्या शोधात असतात.

डायोफंटाईन ते लाग्रांज (मार्गे ऑयलर आणि फर्मा)

पण आपल्याला असं उदाहरण लगेच मिळालं नाही, म्हणून ते अस्तित्वातच नाही, असं म्हणायचा घायकुतेपणा करून चालत नाही. सरतेशेवटी नैसर्गिक संख्या ह्या अनंत आहेत. तुम्ही खरंच अशी फोड होते आहे का, हे एका मर्यादेपर्यंत कॅल्क्युलेटरवर किंवा संगणकावर किंवा महासंगणकावर तपासून पाहाल, पण अशी साधने अनंतकाळपर्यंत चालू शकत नाहीत. त्यामुळे गणितज्ञांना हवी असते, ती सिद्धता! अनंताबद्दलची अशी विधाने प्रत्यक्ष पडताळून पाहू शकत नाही, तर ती तर्कबुद्धीच्या कसोटीवर घासून घ्यावी लागतात. त्यामुळे वरचे विधान हे सध्या आपण फक्त एक कयास (conjecture) म्हणून मांडू शकतो.

कयास (Conjecture) : प्रत्येक नैसर्गिक संख्या ही ४ किंवा त्याहून कमी पूर्णवर्गांच्या बेरजेच्या स्वरूपात मांडता येते.

वरील कयास पहिल्यांदा मांडला, तो खूप आधी. इ. स. २०० च्या आसपास 'डायोफँटस' (Diophantus) नामक एका ग्रीक गणितज्ञाने. (हा माझ्या लेखांत आधीही येऊन गेला आहे.) नंबर थिअरीस्ट्सना आजही प्रेरित करणार्‍या 'अ‍ॅरिथमेटिका' (Arithmetica) ह्या त्याच्या ग्रंथात त्याने वरीलसारखी अनेक उदाहरणे दिली. सतराव्या शतकात १६२५ सालाच्या आसपास 'बाशे' (Bachet) ह्या गणितज्ञाने ह्या ग्रंथाचे लॅटिनमध्ये भाषांतर करताना हा कयास 'सिद्धांत' (Theorem) म्हणून लिहिला. परंतु ह्याची सिद्धता झालेली नव्हती. अत्यंत साध्या व आकर्षक दिसणार्‍या ह्या कयासामागे गणिती लागणे अगदी स्वाभाविक होते, परंतु सिद्धता मिळायला जवळपास १५० वर्षे जावी लागली.

ह्या सिद्धतेच्या मार्गातला महत्वाचा टप्पा म्हणजे 'ऑयलरचा चतुर्वर्गांचा नियम' (Euler's Four Squares Identity). १७४८ साली ऑयलरने गोल्डबाख नामक गणितज्ञाला लिहिलेल्या पत्रात त्याने हा नियम मांडला. थोडक्यात सांगायचे झाल्यास,

जर दोन संख्या 'अ' आणि 'ब' चार पूर्णवर्गांच्या बेरजेच्या स्वरूपात लिहिता येत असतील, तर त्यांचा गुणाकार अब ही संख्यादेखील चार पूर्णवर्गांच्या बेरजेच्या स्वरूपात लिहिता येते!!

ह्या विधानाची एका ओळीत सिद्धता पुढीलप्रमाणे देता येते -

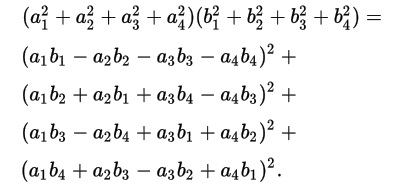
डावीकडे (वर) चार वर्गांची बेरीज असलेल्या दोन संख्यांचा गुणाकार आहे, तर उजवीकडे (खाली) चार वर्गांची बेरीज आहे! a आणि b च्या कुठल्याही किंमतींसाठी हा नियम लागू होत असल्याने, तो अश्या सर्व संख्यांच्या बाबतीत लागू होतो.

वरील नियम हा प्राथमिक नंबर थिअरीमधले नितांतसुंदर विधान आहे. अश्या सर्व अनंत संख्यांना लागू होणारे विधान लिहिणे व लिहिता येणे, ही गोष्ट प्र चं ड महान आहे. मला गणिताकडे खेचण्याकडे ह्या विधानाने व त्यातून प्रतीत होणार्‍या सौंदर्याने मोठी भूमिका बजावली आहे, हे मी येथे नमूद करू इच्छितो.

ह्या नियमाचं एवढं कौतुक काय चालवलंय रे? असं तुमच्या मनात नक्की आलं असेल. काय होतं ह्या नियमाने? तर लक्षात घेऊया, की नैसर्गिक संख्या आपण गुणाकाराने बनवू शकतो, किंवा बेरजेने. आपला मूळ कयास हा गुणाकार ( संख्येचा वर्ग करणे) आणि बेरीज अश्या दोन्ही प्रक्रियांना गुंफणारा कयास आहे. त्यामुळे तो सोडवायला आपल्याला अश्याच गुंफणार्‍या नियमांची मदत घ्यावी लागेल. त्यातून हा नियम आपल्याला सांगतोय, की जर तुम्हाला एक संख्या चार वर्गांची बेरीज म्हणून लिहायची असेल, तर तिच्यापेक्षा छोट्या संख्या चार वर्गांची बेरीज म्हणून लिहिता येतात, का ते बघा. म्हणजे थोडक्यात आपलं काम कमी करतोय. म्हणून हा नियम महत्वाचा आहे.

संख्यांचे गुणाकाराशी निगडित गुणधर्म अभ्यासताना आपली गाठ पडते 'अविभाज्य' अथवा 'मूळ' संख्यांशी. मूळ संख्यांचा एकमेकांशी गुणाकार करूनच तर सगळ्या संख्या बनतात ना! प्रत्येक नैसर्गिक संख्या ही मूळ संख्यांच्या गुणाकाराच्या स्वरूपात लिहिता येते, हेसुद्धा आपण शाळेत घोकायचो. ह्या सगळ्यांमुळे वेगळीच कल्पना गणितज्ञांच्या डोक्यात आली, की जर सगळ्या मूळ संख्या आपण चार वर्गांची बेरीज म्हणून लिहू शकलो, तर आपण ऑयलरचा नियम वापरून त्यांचे गुणाकार आणि पर्यायाने सर्व नैसर्गिक संख्या चार वर्गांची बेरीज म्हणून लिहू शकू की!

कयास २ (Conjecture 2) : प्रत्येक मूळ संख्या ही ४ किंवा त्याहून कमी पूर्णवर्गांच्या बेरजेच्या स्वरूपात मांडता येते.

आपण आता गोष्ट मूळ संख्यांपर्यंत आणली. मूळ संख्या ह्या नैसर्गिक संख्यांहून कमी आहेत, त्यामुळे आपलं काम एका अर्थी कमी झालं. त्याचबरोबर मूळ संख्यांचे गुणधर्म जास्त जोरकस आणि विशेष आहेत, हा फायदा झाला. कदाचित आपण असे गुणधर्म वापरून कयास २ सिद्ध करू, म्हणजे आधीचा कयास ऑयलरच्या नियमामुळे आपोआपच सिद्ध होईल, अशी व्यूहरचना करता येईल.

अशी व्यूहरचना केली खरी, पण तरी कयास २ सिद्ध करायला अजून २ दशके जावी लागली. फर्मा (Fermat) ह्याने कयास २ चा अर्धा भाग आधीच एका वेगळ्या प्रश्नासाठी सिद्ध केला होता. उरलेल्या अर्ध्या भागाची सिद्धता लाग्रांज (Lagrange) ह्याने १७७० मध्ये दिली. आणि आपण काही साध्या उदाहरणांमधून केलेला कयास चातुर्वर्गांचा सिद्धांत (Four Squares Theorem) म्हणून मान्यता पावला.

सिद्धांत (Theorem) : प्रत्येक नैसर्गिक संख्या ही ४ किंवा त्याहून कमी पूर्णवर्गांच्या बेरजेच्या स्वरूपात मांडता येते.

कयास २ च्या सिद्धतेबद्दल मी येथे विस्तारभयास्तव लिहिणार नाही, पण ह्या सिद्धतेमधून नंबर थिअरी आणि गणिताच्या विकासास पूरक अशा अनेक पद्धती उगम पावल्या. क्वाटर्नियन्सच्या कल्पनेबद्दल उदाहरणार्थ इंजिनीयरिंगमध्ये तुम्ही शिकला असाल, तर त्या कल्पनेची एक प्रेरणा ह्या सिद्धांतामधून आली आहे, हे नमूद करतो. चांगले प्रश्न विचारल्यास ज्ञानाचा विकास होतो तो असा.

पुढे?

वर्गांवरच का थांबायचं? घनांच्या (तृतीय घातांच्या) बेरजा का नाही? चतुर्थ घातांच्या का नाही? असे प्रश्न पडणे स्वाभाविक आहे. ह्यातूनच 'वेरिंग' नामक गणितज्ञाने घात {n} आणि सर्व नैसर्गिक संख्यांची फोड करण्यास घातांची लागणारी संख्या {g(n)} ह्यांची सांगड घालणारा कयास मांडला. (उदा. वरील सिद्धांतानुसार g(2) = 4.) मग g(3) = किती? असा कयास मांडला गेला.

उदा. २३ = ८ + ८ + १ + १ + १ + १ + १ + १ + १ अशीच घनांमध्ये फोड होऊ शकते. त्यामुळे g(3) > 8 हे नक्की.

ह्याही प्रश्नावर बरेच काम झाले. शेवटी विफ्रिश आणि केंपनर ह्यांनी g(3) = 9 हे सिद्ध केले. आर. बालसुब्रमणियन हे भारतीय गणितज्ञ आणि देश्वे हे फ्रेंच गणितज्ञ ह्यांच्या कामातून g(4) =19 हे सिद्ध झाले. ह्या दिशेने इतर संख्यांसाठी सिद्धता देण्यावर अजूनही काम चालू आहे.

अश्या प्रकारे अत्यंत साध्या, अगदी लहान मुलांबरोबर संख्यांशी खेळू शकणार्‍या प्रश्नांमुळे गणिताची अनेक प्रकारे प्रगती झाली आहे. अनेक गणितज्ञांना अश्या प्रश्नांनी प्रेरित केले आहे. अश्या प्रश्नाची तुम्हाला ओळख करून द्यावीशी वाटली.